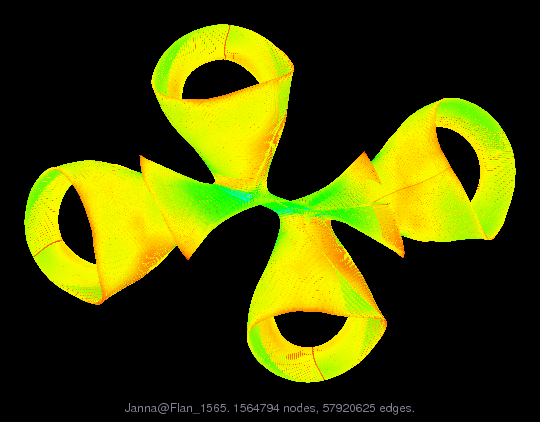
Matrix: Janna/Flan_1565
Description: 3D model of a steel flange, hexahedral finite elements
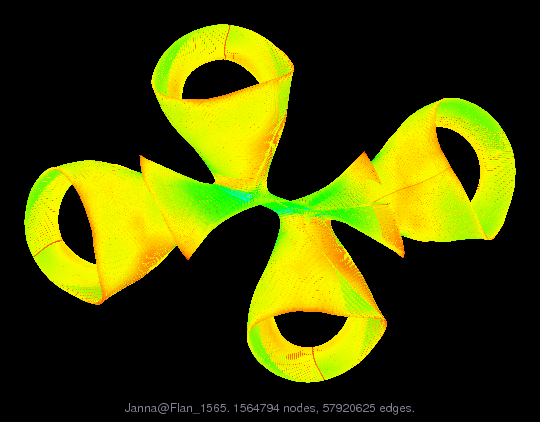 |
| (undirected graph drawing) |
 |
| Matrix properties | |
| number of rows | 1,564,794 |
| number of columns | 1,564,794 |
| nonzeros | 114,165,372 |
| structural full rank? | yes |
| structural rank | 1,564,794 |
| # of blocks from dmperm | 1 |
| # strongly connected comp. | 1 |
| explicit zero entries | 3,240,672 |
| nonzero pattern symmetry | symmetric |
| numeric value symmetry | symmetric |
| type | real |
| structure | symmetric |
| Cholesky candidate? | yes |
| positive definite? | yes |
| author | C. Janna, M. Ferronato |
| editor | T. Davis |
| date | 2011 |
| kind | structural problem |
| 2D/3D problem? | yes |
Notes:
Authors: Carlo Janna and Massimiliano Ferronato
Symmetric Positive Definite Matrix
# equations: 1564794
# non-zeroes: 117406044
Problem description: Structural problem
The matrix Flan_1565 is obtained from a 3D mechanical problem
discretizing a steel flange with hexahedral Finite Elements. Due
to the regular shape of the mechanical piece, the computational
grid is a structured mesh with regularly shaped elements. Three
displacement unknowns are associated to each node of the grid.
Some further information may be found in the following papers:
1) C. Janna, A. Comerlati, G. Gambolati. "A comparison of
projective and direct solvers for finite elements in
elastostatics". Advances in Engineering Software, 40, pp.
675-685, 2009.
2) C. Janna, M. Ferronato, G. Gambolati. "A Block FSAI-ILU
parallel preconditioner for symmetric positive definite linear
systems". SIAM Journal on Scientific Computing, 32, pp.
2468-2484, 2010.
| Ordering statistics: | result |
| nnz(chol(P*(A+A'+s*I)*P')) with AMD | 3,651,940,140 |
| Cholesky flop count | 2.2e+13 |
| nnz(L+U), no partial pivoting, with AMD | 7,302,315,486 |
| nnz(V) for QR, upper bound nnz(L) for LU, with COLAMD | 6,488,489,176 |
| nnz(R) for QR, upper bound nnz(U) for LU, with COLAMD | 12,183,623,118 |
Note that all matrix statistics (except nonzero pattern symmetry) exclude the 3240672 explicit zero entries.
For a description of the statistics displayed above, click here.
Maintained by Tim Davis, last updated 12-Mar-2014.
Matrix pictures by cspy, a MATLAB function in the CSparse package.
Matrix graphs by Yifan Hu, AT&T Labs Visualization Group.