Intent:

This pattern is used to describe concurrent execution by a collection of independent tasks. Parallel Algorithms that use this pattern are called embarrassingly parallel because once the tasks have been defined the potential concurrency is obvious.

Also Known As:

• Master-Worker.
• Task Queue.

Motivation:

Consider an algorithm that can be decomposed into many independent tasks. Such an algorithm, often called an "embarrassingly parallel" algorithm, contains obvious concurrency that is trivial to exploit once these independent tasks have been defined, because of the independence of the tasks. Nevertheless, while the source of the concurrency is often obvious, taking advantage of it in a way that makes for efficient execution can be difficult.

The EmbarrassinglyParallel pattern shows how to organize such a collection of tasks so they execute efficiently. The challenge is to organize the computation so that all units of execution finish their work at about the same time -- that is, so that the computational load is balanced among processors. The following figure illustrates the problem.

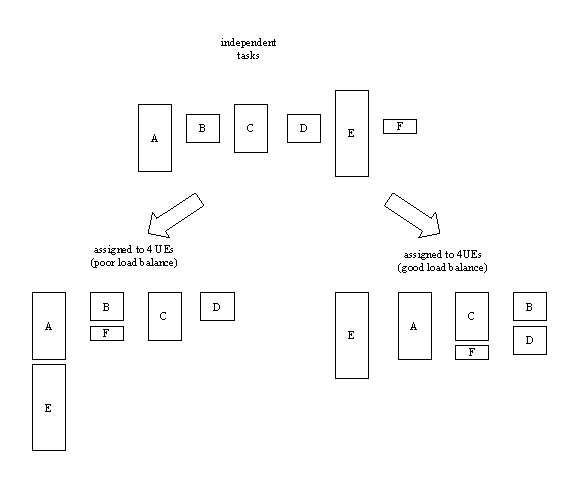
This pattern automatically and dynamically balances the load as necessary. With this pattern, faster or less-loaded UEs automatically do more work. When the amount of work required for each task cannot be predicted ahead of time, this pattern produces a statistically optimal solution.

Examples of this pattern include the following:

• Vector addition (considering the addition of each pair of elements as a separate task).
• Ray-tracing codes such as the medical-imaging example described in the DecompositionStrategy pattern. Here the computation associated with each "ray" becomes a separate task.
• Database searches in which the problem is to search for an item meeting specified criteria in a database that can be partitioned into subspaces that can be searched concurrently. Here the searches of the subspaces are the independent tasks.
• Branch-and-bound computations, in which the problem is solved by repeatedly removing a solution space from a list of such spaces, examining it, and either declaring it a solution, discarding it, or dividing it into smaller solution spaces that are then added to the list of spaces to examine. Such computations can be parallelized using this pattern by making each "examine and process a solution space" step a separate task.

As these examples illustrate, this pattern allows for a fair amount of variation: The tasks can all be roughly equal in size, or they can vary in size. Also, for some problems (the database search, for example), it may be possible to solve the problem without executing all the tasks. Finally, for some problems (branch-and-bound computations, for example), new tasks may be created during execution of other tasks.

Observe that although frequently the source of the concurrency is obvious (hence the name of the pattern), this pattern also applies when the source of the concurrency requires some insight to discover; the distinguishing characteristic of problems using this pattern is the complete independence of the tasks.

More formally, the EmbarrassinglyParallel pattern is applicable when what we want to compute is a solution(P) such that

    solution(P) =
        f(subsolution(P, 0),
          subsolution(P, 1), ...,
          subsolution(P, N-1))

such that for i and j different, subsolution(P, i) does not depend on subsolution(P, j). That is, the original problem can be decomposed into a number of independent subproblems such that we can solve the whole problem by solving all of the subproblems and then combining the results. We could code a sequential solution thus:

    Problem P;
    Solution subsolutions[N];
    Solution solution;
    for (i = 0; i < N; i++) {
        subsolutions[i] = 
            compute_subsolution(P, i);
    }
    solution = 
        compute_f(subsolutions);

If function compute_subsolution modifies only local variables, it is straightforward to show that the sequential composition implied by the for loop in the preceding program can be replaced by any combination of sequential and parallel composition without affecting the result. That is, we can partition the iterations of this loop among available UEs in whatever way we choose, so long as each is executed exactly once.

This is the EmbarrassinglyParallel pattern in its simplest form -- all the subproblems are defined before computation begins, and each subsolution is saved in a distinct variable (array element), so the computation of the subsolutions is completely independent. These computations of subsolutions then become the independent tasks of the pattern as described earlier.

There are also some variations on this basic theme:

• Subsolutions accumulated in a shared data structure. One such variation differs from the simple form in that it accumulates subsolutions in a shared data structure (a set, for example, or a running sum). Computation of subsolutions is no longer completely independent (since access to the shared data structure must be synchronized), but concurrency is still possible if the order in which subsolutions are added to the shared data structure does not affect the result.
• Termination condition other than "all tasks complete". In the simple form of the pattern, all tasks must be completed before the problem can be regarded as solved, so we can think of the parallel algorithm as having the termination condition "all tasks complete". For some problems, however, it may be possible to obtain an overall solution without solving all the subproblems. For example, if the whole problem consists of determining whether a large search space contains at least one item meeting given search criteria, and each subproblem consists of searching a subspace (where the union of the subspaces is the whole space), then the computation can stop as soon as any subspace is found to contain an item meeting the search criteria. As in the simple form of the pattern, each computation of a subsolution becomes a task, but now the termination condition is something other than "all tasks completed". This can also be made to work, although care must be taken to either ensure that the desired termination condition will actually occur or to make provision for the case in which all tasks are completed without reaching the desired condition.
• Not all subproblems known initially. A final and more complicated variation differs in that not all subproblems are known initially; that is, some subproblems are generated during solution of other subproblems. Again, each computation of a subsolution becomes a task, but now new tasks can be created "on the fly". This imposes additional requirements on the part of the program that keeps track of the subproblems and which of them have been solved, but these requirements can be met without too much trouble, for example by using a thread-safe shared task queue. The trickier problem is ensuring that the desired termination condition ("all tasks completed" or something else) will eventually be met.

What all of these variations have in common, however, is that they meet the pattern's key restriction: It must be possible to solve the subproblems into which we partition the original problem independently. Also, if the subsolution results are to be collected into a shared data structure, it must be the case that the order in which subsolutions are placed in this data structure does not affect the result of the computation.

Applicability:

Use the EmbarrassinglyParallel pattern when:

• The problem consists of tasks that are known to be independent; that is, there are no data dependencies between tasks (aside from those described in "Subsolutions accumulated in a shared data structure" above).

This pattern can be particularly effective when:

• The startup cost for initiating a task is much less than the cost of the task itself.
• The number of tasks is much greater than the number of processors to be used in the parallel computation.
• The effort required for each task or the processing performance of the processors varies unpredictably. This unpredictability makes it very difficult to produce an optimal static work distribution.

Structure:

Implementations of this pattern include the following key elements:

• A mechanism to define a set of tasks and schedule their execution onto a set of UEs.
• A mechanism to detect completion of the tasks and terminate the computation.

Usage:

This pattern is typically used to provide high-level structure for an application; that is, the application is typically structured as an instance of this pattern. It can also be used in the context of a simple sequential control structure such as sequential composition, if-then-else, or a loop construct. An example is given in our overview paper, where the program as a whole is a simple loop whose body contains an instance of this pattern.

Consequences:

The EmbarrassinglyParallel pattern has some powerful benefits, but also a significant restriction.

• Parallel programs that use this pattern are among the simplest of all parallel programs. If the independent tasks correspond to individual loop iterations and these iterations do not share data dependencies, parallelization can be easily implemented with a parallel loop directive.
• With some care on the part of the programmer, it is possible to implement programs with this pattern that automatically and dynamically adjust the load between units of execution. This makes the EmbarrassinglyParallel pattern popular for programs designed to run on parallel computers built from networks of workstations.
• This pattern is particularly valuable when the effort required for each task varies significantly and unpredictably. It also works particularly well on heterogeneous networks, since faster or less-loaded processors naturally take on more of the work.
• The downside, of course, is that the whole pattern breaks down when the tasks need to interact during their computation. This limits the number of applications where this pattern can be used.

Implementation:

There are many ways to implement this pattern. If all the tasks are of the same size, all are known a priori, and all must be completed (the simplest form of the pattern), the pattern can be implemented by simply dividing the tasks among units of execution using a parallel loop directive. Otherwise, it is common to collect the tasks into a queue (the task queue) shared among UEs. This task queue can then be implemented using the SharedQueue pattern. The task queue, however, can also be represented by a simpler structure such as a shared counter.

Key elements.

Defining tasks and scheduling their execution.

A set of tasks is represented and scheduled for execution on multiple units of execution (UEs). Frequently the tasks correspond to iterations of a loop. In this case we implement this pattern by splitting the loop between multiple UEs. The key to making algorithms based on this pattern run well is to schedule their execution so the load is balanced between the UEs. The schedule can be:

• Static. In this case the distribution of iterations among the UEs is determined once, at the start of the computation. This might be an effective strategy when the tasks have a known amount of computation and the UEs are running on systems with a well-known and stable load. In other words, a static schedule works when you can statically determine how many iterations to assign to each UE in order to achieve a balanced load. Common options are to use a fixed interleaving of tasks between UEs, or a blocked distribution in which blocks of tasks are defined and distributed, one to each UE.
• Dynamic. Here the distribution of iterations varies between UEs as the computation proceeds. This strategy is used when the effort associated with each task is unpredictable or when the available load that can be supported by each UE is unknown and potentially changing. The most common approach used for dynamic load balancing is to define a task queue to be used by all the UEs; when a UE completes its current task and is therefore ready to process more work, it removes a task from the task queue. Faster UEs or those receiving lighter-weight tasks will go to the queue more often and automatically grab more tasks.

Implementation techniques include parallel loops and master-worker and SPMD versions of a task-queue approach.

Parallel loop.

If the computation fits the simplest form of the pattern -- all tasks the same size, all known a priori, and all required to be completed -- they can be scheduled by simply setting up a parallel loop that divides them equally (or as equally as possible) among the available units of execution.

Master-Worker or SPMD.

If the computation does not fit the simplest form of the pattern, the most common implementation involves some form of a task queue. Frequently this is done using two types of processes, master and worker. There is only one master process; it manages the computation by:

• Setting up or otherwise managing the workers.
• Creating and managing a collection of tasks (the task queue).
• Consuming results.

There can be many worker processes; each contains some type of loop that repeatedly:

• Removes the task at the head of the queue.
• Carries out the indicated computation.
• Returns the result to the master.

Frequently the master and worker processes form an instance of the ForkJoin pattern, with the master process forking off a number of workers and waiting for them to complete.

A common variation is to use an SPMD program with a global counter to implement the task queue. This form of the pattern does not require an explicit master.

Detecting completion and terminating.

Termination can be implemented in a number of ways.

If the program is structured using the ForkJoin pattern, the workers can continue until the termination condition is reached, checking for an empty task queue (if the termination condition is "all tasks completed") or for some other desired condition. As each worker detects the appropriate condition, it terminates; when all have terminated, the master continues with any final combining of results generated by the individual tasks.

Another approach is for the master or a worker to check for the desired termination condition and, when it is detected, create a "poison pill", a special task that tells all the other workers to terminate.

Correctness considerations.

The keys to exploiting available concurrency while maintaining program correctness (for the problem in its simplest form) are as follows.

• Solve subproblems independently. Computing the solution to one subproblem must not interfere with computing the solution to another subproblem. This can be guaranteed if the code that solves each subproblem does not modify any variables shared between units of execution (UEs).
• Solve each subproblem exactly once. This is almost trivially guaranteed if static scheduling is used (i.e., if the tasks are scheduled via a parallel loop). It is also easily guaranteed if the parallel algorithm is structured as follows:
• A task queue is created as an instance of a thread-safe shared data structure such as SharedQueue, with one entry representing each task.
• A collection of UEs execute concurrently; each repeatedly removes a task from the queue and solves the corresponding subproblem.
• When the queue is empty and each UE finishes the task it is currently working on, all the subsolutions have been computed, and the algorithm can proceed to the next step, combining them. (This also means that if a UE finishes a task and finds the task queue empty, it knows that there is no more work for it to do, and it can take appropriate action -- terminating if there is a master UE that will take care of any combining of subsolutions, for example.)
• Correctly save subsolutions. This is trivial if each subsolution is saved in a distinct variable, since there is then no possibility that the saving of one subsolution will affect subsolutions computed and saved by other tasks.
• Correctly combine subsolutions. This can be guaranteed by ensuring that the code to combine subsolutions does not begin execution until all subsolutions have been computed as discussed above.

The variations mentioned earlier impose additional requirements:

• Subsolutions accumulated in a shared data structure. If the subsolutions are to be collected into a shared data structure, then the implementation must guarantee that concurrent access does not damage the shared data structure. This can be ensured by implementing the shared data structure as an instance of a "thread-safe" pattern.
• Termination condition other than "all tasks complete". Then the implementation must guarantee that each subsolution is computed at most once (easily done by using a task queue as described earlier) and that the computation detects the desired termination condition and terminates when it is found. This is more difficult but still possible.
• Not all subproblems known initially. Then the implementation must guarantee that each subsolution is computed exactly once, or at most once (depending on the desired termination condition.) Also, the program designer must ensure that the desired termination detection will eventually be reached. For example, if the termination condition is "all tasks completed", then the pool generated must be finite, and each individual task must terminate. Again, a task queue as described earlier solves some of the problems; it will be safe for worker UEs to add as well as remove elements. Detecting termination of the computation is more difficult, however. It is not necessarily the case that when a "worker" finishes a task and finds the task queue empty that there is no more work to do -- another worker could generate a new task. One must therefore ensure that the task queue is empty and all workers are finished. Further, in systems based on asynchronous message passing, one must also ensure that there are no messages in transit that could, on their arrival, create a new task. There are many known algorithms that solve this problem. One that is useful in this context is described in [Dijkstra80]. Here tasks conceptually form a tree, where the root is the master task, and the children of a task are the tasks it generated. When a task and all its children have terminated, it notifies its parent that it has terminated. When all the children of the root have terminated, the computation has terminated. This of course requires children to keep track of their parents and to notify them when they are finished. Parents must also keep track of the number of active children (the number created minus the number that have terminated). Additional algorithms for termination detection are described in [Bertsekas89].

Efficiency considerations.

• If all tasks are roughly the same length and their number is known a priori, static scheduling (usually performed using a parallel loop directive) is likely to be more efficient than dynamic scheduling.
• If a task queue is used, put the longer tasks at the beginning of the queue if possible. This ensures that there will be work to overlap with their computation.

Examples:

Vector addition.

Consider a simple vector addition, say C = A + B. As discussed earlier, we can consider each element addition (C_i = A_i + B_i) as a separate task and parallelize this computation in the form of a parallel loop:

• See the section "Vector Addition" in the examples document.

Varying-length tasks.

Consider a problem consisting of N independent tasks. Assume we can map each task onto a sequence of simple integers ranging from 0 to N-1. Further assume that the effort required by each task varies considerably and is unpredictable. Several implementations are possible, including:

• A master-worker implementation using a task queue. See the section "Varying-Length Tasks, Master-Worker Implementation" in the examples document.
• An SPMD implementation using a task queue. See the section "Varying-Length Tasks, SPMD Implementation" in the examples document.

Optimization.

See our overview paper for an extended example using this pattern.

Known Uses:

There are many application areas in which this pattern is useful. Many ray-tracing codes use some form of partitioning with individual tasks corresponding to scan lines in the final image [Bjornson91a]. Applications coded with the Linda coordination language are another rich source of examples of this pattern [Bjornson91b].

Parallel computational chemistry applications also make heavy use of this pattern. In the quantum chemistry code GAMESS, the loops over two electron integrals are parallelized with the TCGMSG task queue mechanism mentioned earlier. An early version of the Distance Geometry code, DGEOM, was parallelized with the Master-Worker form of the EmbarrassinglyParallel pattern. These examples are discussed in [Mattson95b].

Related Patterns:

The SeparableDependencies pattern is closely related to the EmbarrassinglyParallel pattern. To see this relation, think of the SeparableDependencies pattern in terms of a three-phase approach to the parallel algorithm. In the first phase, dependencies are pulled outside a set of tasks, usually by replicating shared data and converting it into task-local data. In the second phase, the tasks are run concurrently as completely independent tasks. In the final phase, the task-local data is recombined (reduced) back into the original shared data structure.

The middle phase of the SeparableDependencies pattern is an instance of the EmbarrassinglyParallel pattern. That is, you can think of the SeparableDependencies pattern as a technique for converting problems into embarrassingly parallel problems. This technique can be used in certain cases with most of the other patterns in our pattern language. The key is that the dependencies can be pulled outside of the concurrent execution of tasks. If this isolation can be done, then the execution of the tasks can be handled with the EmbarrassinglyParallel pattern.

Many instances of the GeometricDecomposition pattern (for example, "mesh computations" in which new values are computed for each point in a grid based on data from nearby points) can be similarly viewed as two-phase computations, where the first phase consists of exchanging boundary information among UEs and the second phase is an instance of the EmbarrassinglyParallel pattern in which each UE computes new values for the points it "owns".

It is also worthwhile to note that some problems in which the concurrency is based on a geometric data decomposition are, despite the name, not instances of the GeometricDecomposition pattern but instances of EmbarrassinglyParallel. An example is a variant of the vector addition example presented earlier, in which the vector is partitioned into "chunks", with computation for each "chunk" treated as a separate task.