Berna L. Massingill, Timothy G. Mattson, Beverly A. Sanders
Parallel computing has failed to attract significant numbers of programmers outside the specialized world of supercomputing. This is due in part to the fact that despite the best efforts of many researchers, parallel programming environments are so hard to use that most programmers won't risk using them. We believe the major cause for this state of affairs is that most parallel programming environments focus on how concurrency is implemented rather than on how concurrency is exploited in a program design. In other words, bringing parallel computing to a broader audience requires solving the problem at the algorithm design level.
For software development in general, the use of design patterns has emerged as an effective way to help programmers design high-quality software. To be most useful, patterns that work together to solve design problems are collected into structured hierarchical catalogs called pattern languages. A pattern language helps guide programmers through the whole process of application design and development.
We believe this approach can be usefully applied to parallel computing; that is, that we can make parallel programming attractive to general-purpose professional programmers by providing them with a pattern language for parallel application programming.
In this paper we provide an early look at our ongoing research into producing such a pattern language. We describe its overall structure, present a complete example of one of our patterns, and show how it can be used to develop a parallel global optimization application.
Parallel hardware has been available for some decades now and is becoming increasingly mainstream. Software that takes advantage of these machines, however, is much rarer, largely because of the widespread and justified belief that such software is too difficult to write. Most research to date on making parallel machines easier to use has focused on the creation of parallel programming environments that hide the details of a particular computer system from the programmer, making it possible to write portable software; a good example of this sort of programming environment is MPI [MPI]. These environments have been successful overall in meeting the needs of the high-performance computing (HPC) community. Outside the HPC community, however, only a small fraction of programmers would even consider writing parallel software, so research into parallel programming environments cannot be considered a general success, and indeed this research seems to focus on the HPC community at the expense of the rest of the programming world.
The reasons for this state of affairs are complex. We believe the fault lies with the parallel programming environments, but we do not believe that they can be fixed with yet another high-level abstraction of a parallel computer. To get professional programmers to write parallel software, we must give them a programming environment that helps them understand and express the concurrency in an algorithm. In other words, we need to solve this problem at the level of algorithm design.
At the same time, theoretical computer scientists have developed a substantial body of work that can be used to formally demonstrate correctness of parallel programs. Given the difficulty of debugging parallel programs, it would clearly be of benefit to programmers to help them avoid bugs in the first place, and what has been learned by the theoreticians could be of help in that regard --- if it can be presented in a way that is accessible to professional programmers, which so far has not generally been the case.
Helping programmers design high-quality software is a general problem in software engineering. Currently, one of the most popular solutions is based on design patterns [Gamma95]. A design pattern is a carefully-written solution to a recurring software design problem. These patterns are usually organized into a hierarchical catalog of patterns. Software designers can use such a pattern catalog to guide themselves from problem specifications to complete designs. This collection of patterns is called a pattern language. An effective pattern language goes beyond the patterns themselves and provides guidance to the designer about how to use the patterns.
Design patterns have had a major impact on modern software design. We believe the same approach can be used to help programmers write parallel software. That is, we believe that we can attract the general-purpose professional programmer to parallel computing if we give them a pattern language for parallel application programming. We also believe that such a pattern language can incorporate some of what has been learned by the theoretical community in a way that benefits our target audience.
In this paper, we provide an early view of our ongoing research ([Massingill99]) into producing a pattern language for parallel application programming. We begin by considering related work on skeletons, frameworks, and archetypes. We then give an overview of our pattern language and its overall structure. Finally, we show how our pattern language can be used to write a parallel global optimization application. In the appendices, we describe the notation we use for expressing patterns and present an example design pattern.
Considerable work has been done in identifying and exploiting patterns to facilitate software development, on levels ranging from overall program structure to detailed design. The common theme of all of this work is that of identifying a pattern that captures some aspect of effective program design and/or implementation and then reusing this design or implementation in many applications.
Algorithmic skeletons, first described in [Cole89], capture very high-level patterns; they are frequently envisaged as higher-order functions that provide overall structure for applications, with each application supplying lower-level code specific to the application. The emphasis is on design reuse, although work has been done on implementing program skeletons.
Program frameworks ([Coplien95]) similarly address overall program organization, but they tend to be more detailed and domain-specific, and they provide a range of low-level functions and emphasize reuse of code as well as design.
Design patterns, in contrast to skeletons and frameworks, can address design problems at many levels, though most existing patterns address fairly low-level design issues. They also emphasize reuse of design rather than reuse of code; indeed, they typically provide only a description of the pattern together with advice on its application. One of the most immediately useful features of the design patterns approach is simply that it gives program designers and developers a common vocabulary, since each pattern has a name. Early work on patterns (e.g., [Gamma95]) dealt mostly with object-oriented sequential programming, but more recent work ([Schmidt93]) addresses parallel programming as well, though mostly at a fairly low level. Work explicitly aimed at organizing patterns into pattern languages seems to be less common though not unknown, as some of the examples referenced at [Patterns98] indicate.
Programming archetypes ([Chandy94], [Massingill96]) combine elements of all of the above categories: They capture common computational and structural elements at a high level, but they also provide a basis for implementations that include both high-level frameworks and low-level code libraries. A parallel programming archetype combines a computational pattern with a parallelization strategy; this combined pattern can serve as a basis both for designing and reasoning about programs (as a design pattern does) and for code skeletons and libraries (as a framework does). Archetypes do not, however, directly address the question of how to choose an appropriate archetype for a particular problem.
A design pattern is a solution to a problem in a context. We find design patterns by looking at high-quality solutions to related problems; the design pattern is written down in a systematic way and captures the common elements that distinguish good solutions from poor ones.
We can design complex systems in terms of patterns. At each decision point, the designer selects the appropriate pattern from a pattern catalog. Each pattern leads to other patterns, resulting in a final design in terms of a web of patterns. A structured catalog of patterns that supports this design style is called a pattern language. A pattern language is more than just a catalog of patterns; it embodies a design methodology and provides domain-specific advice to the application designer. (Despite the overlapping terminology, however, note that our pattern language is not a programming language but rather a structured collection of language-independent patterns.)
The pattern language described in this document is intended for application programmers who want to design new programs for execution on parallel computers. The top-level patterns help the designer decide how to decompose a problem into components that can run concurrently. The lower-level patterns help the designer express this concurrency in terms of parallel algorithms and finally at the lowest level in terms of the parallel environment's primitives. These lower levels of our pattern language correspond to entities not usually considered to be patterns. We include them in our pattern language, however, so that the language is better able to provide a complete path from problem description to code, and we describe them using our pattern notation in order to provide a consistent interface for the programmer.
Our pattern language addresses only concurrency; it is meant to complement rather than replace other pattern-based design systems. Before programmers can work with this pattern language, they must understand the core objects, mathematics, and abstract algorithms involved with their problems. In this pattern language, we refer to design activities that take place in the problem domain and outside of this pattern language as reasoning in the problem space. The pattern language will use the results from problem space reasoning, but it will not help the programmer carry it out.
Before plunging into the structure of our pattern language, we offer one additional observation. In addition to facilitating reuse of code and design, patterns allow for a certain amount of "proof reuse": A pattern can include a careful specification for its application-specific parts, such that a use of the pattern that meets that specification is known to be correct by virtue of a proof done once for the pattern. Patterns that include implementation can also have their implemented parts proved correct. Thus, patterns can serve as a vehicle for making some results from the theoretical community accessible and useful for programmers; our pattern language takes advantage of this.
Our pattern language is organized around four core design spaces arranged in a linear hierarchy. The higher-level spaces correspond to an abstract view of parallel programming, independent of particular target environments; lower-level spaces are more implementation-specific, with the lowest-level space a pattern-based description of the low-level building blocks used to construct parallel programs in particular target environments. To use our pattern language, application designers begin at the top level and work their way down, transforming problem descriptions into parallel algorithms and finally into parallel code.
The contents of the two top-level design spaces are relatively mature. The lower two levels, however, are still under development and will almost certainly change as we work through more examples using our pattern language.
This space is concerned with exposing exploitable concurrency. That is, the patterns in this space help programmers decompose their problems into concurrently-executable units of work. The issues addressed at this level are at a high level and are well removed from specific implementation issues.
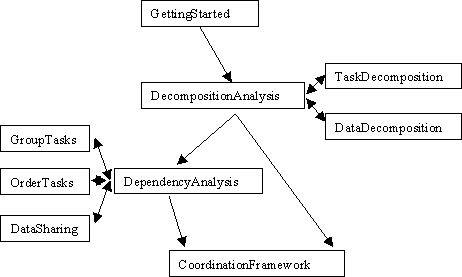
Figure 1 shows the patterns in this design space and how they would be used by an algorithms designer or programmer.

Figure 1: This figure lists the patterns in the FindingConcurrency design space. Starting at the top, the arrows show how a designer would work through the patterns as they define the exploitable concurrency in a software design.
The path through this space begins with the GettingStarted pattern, which tells the designer how to organize the information he or she has about the problem under consideration. The next step is to decompose the problem into relatively independent units. There are two parts to this analysis, an analysis by task (TaskDecomposition) and an analysis by data (DataDecomposition). As the double arrows suggest, the designer may need to cycle between these two decompositions before a final decomposition is found.
Once a problem has been decomposed, the designer must decide how the tasks depend on each other. This is done by cycling between three patterns. The GroupTasks pattern helps the designer collect tasks into groups whose elements must execute concurrently. The OrderTasks pattern then helps order tasks (or task groups) based on data or temporal dependencies. Finally, the DataSharing pattern helps identify how data must be shared among tasks.
The last stop in this design space is the CoordinationFramework pattern, which is really just a consolidation point to make sure the designer has correctly used the patterns in this design space.
This design space is concerned with the high-level structure of the parallel algorithm and overall strategies for exploiting concurrency. The designer working in this space reasons about how to use the concurrency exposed in the FindingConcurrency design space.
The patterns in this space are organized by means of a decision tree, as shown in Figure 2, that helps lead the designer to the patterns that apply to his or her problem.
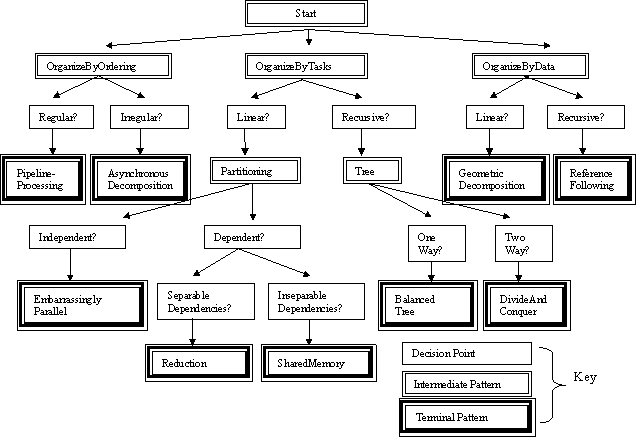
Figure 2: The terminal patterns in this figure are the ones used in an algorithm design. The decision tree in this figure shows the reasoning process a designer would use to arrive at a particular terminal pattern.
The tree in Figure 2 has three types of boxes: intermediate patterns, decision points, and terminal patterns. The intermediate patterns help the designer navigate through the design space. The decision point boxes represent decisions made about the concurrency within the intermediate patterns. Finally, terminal patterns correspond to patterns that will be used in the parallel algorithm.
Starting at the top of the tree, the designer first chooses a top-level organization. There are three choices at this point, resulting in three major branches to the tree: Concurrency can be organized in terms of the temporal ordering of the task groups, in terms of the problem's task decomposition, or in terms of the problem's data decomposition.
The first major branch of the tree, the one below the "OrganizeByOrdering" pattern, has two main subbranches that represent two choices about how the ordering is structured. One choice represents "regular" orderings that do not change during the algorithm; the other represents "irregular" orderings that are more dynamic and unpredictable. These two choices correspond to two terminal patterns:
The second branch ("OrderByTasks"), containing patterns based on the task decomposition, is the most complex branch of the tree. Two choices are available to the designer, based on whether the tasks are structured as linear collections of tasks or recursively.
The first subbranch (which we call Partitioning patterns) in turn splits into two branches, one in which the tasks execute independently (the EmbarrassinglyParallel pattern) and one in which the there are dependencies among tasks. We further split the latter branch based on whether the dependencies can be pulled out of the concurrent execution (the separable case) or whether they must be explicitly managed within the concurrent execution (the inseparable case). This leads to the following terminal patterns:
Moving back up the tree of Figure 2 to the branch corresponding to recursive task structures, we have two cases to consider:
Again moving back up the tree, we look at the third major branch ("OrderByData"), which corresponds to problems in which the concurrency is best understood in terms of data decomposition. Here there are two cases, corresponding to linear and recursive data structures:
By working through this tree until one or more terminal patterns are reached, the designer decides how to structure a parallel algorithm to exploit the concurrency in his or her problem.
This design space is concerned with lower-level constructs used to implement patterns in the AlgorithmStructure space. There are two groups of patterns in this space: those that represent program-structuring constructs (such as SPMD) and those that represent commonly-used shared data structures (such as SharedQueue). We observe again that many of the elements of this design space are not usually thought of as patterns, and indeed some of them (SharedQueue, for example) would ideally be provided to the programmer as part of a framework of reusable software components. We nevertheless document them as patterns, for two reasons: First, as noted earlier, documenting all the elements of our pattern language as patterns provides a consistent notation for the programmer. Second, the existence of such pattern descriptions of components provides guidance for programmers who might need to create their own implementations.
As mentioned earlier, we expect the contents of this design space to change as we gain experience with the pattern language. In particular, the list of shared data structures is incomplete; eventually, it should expand to include all major shared data structures.
The following patterns represent common program structures:
The following patterns represent common shared data structures:
This design space is concerned with the low-level details of how tasks coordinate their behavior. We use it to provide pattern-based descriptions of common mechanisms for process/thread management (e.g., creating or destroying processes/threads) and process/thread interaction (e.g., monitors or message-passing). The members of this design space are largely used to implement the patterns from the higher-level design spaces. While the other design spaces are high-level and do not constrain the programmer to a particular programming environment, the patterns in this design space are much closer to the underlying mechanisms used to implement the design. Patterns in this design space, like those in the SupportingStructures space, describe entities that strictly speaking are not patterns at all. As noted previously, however, we include them in our pattern language to provide a complete path from problem description to code, and we document them using our pattern notation for the sake of consistency. The following are examples of patterns in this space.
As with the SupportingStructures design space, the patterns in the ImplementationMechanisms design space will evolve as we gain experience with our pattern language. The goal is to have a sufficiently complete set of constructs with only minimal overlap of functionality.
As an example of using our pattern language to design a parallel algorithm, we will look at a particular type of global optimization algorithm. This algorithm uses the properties of interval arithmetic [Moore79] to construct a reliable global optimization algorithm.
Intervals provide an alternative representation of floating point numbers. Instead of a single floating point number, a real number is represented by a pair of numbers that bound the real number. The arithmetic operations produce interval results that are guaranteed to bound the mathematically "correct" result. This arithmetic system is robust and safe from numerical errors associated with the inevitable rounding that occurs with floating point arithmetic.
One can express most functions in terms of intervals to produce interval extensions of the functions. Values of the interval extension are guaranteed to bound the mathematically rigorous values of the function. This fact can be used to define a class of global optimization algorithms [Moore92] that find rigorous global optima. The details go well beyond the scope of this paper. The structure of the algorithm however, can be fully appreciated without understanding the details of interval arithmetic.
To make the presentation easier, consider the minimization of an objective function. This function contains a number of parameters that we want to investigate to find the values that yield a minimum value for the function. This problem is complicated by the fact that there may be zero or many sets of such parameter values. A value that is a minimum over some neighborhood may in fact be larger than the values in a nearby neighborhood.
We can visualize the problem by associating an axis in a multidimensional space with each variable parameter. A candidate set of parameters defines a box in this multidimensional space. We start with a single box covering the domain of the function. The box is tested to see if it can contain one or more minima. If the box cannot contain a minimum value, we reject the box. If it can contain a minimum value, we split the box into smaller sub-boxes and put them on a list of candidate boxes. (We will refer to this part of the computation as a "test-and-split-box calculation".) We then continue for each box on the list until either there are no remaining boxes or the remaining boxes are sufficiently small. (We will call testing for this condition the "convergence test".) Pseudocode for this algorithm is given in Figure 3. For efficiency reasons we perform the convergence test only after testing and splitting all boxes, and we therefore keep two lists, one for boxes that have not yet been examined and another for the results of any box-splitting operations.
int done = FALSE;
Interval_box B;
List_of_boxes InList, ResultList;
InList = Initialize();
While (!done){
While (!empty(InList)) {
B = get_next_box(InList);
if (has_minima(B))
split_and_put (B, ResultList);
}
done = convergence_test(ResultList);
copy(ResultList, InList);
}
output(InList);
Figure 3: Pseudocode for the sequential global optimization algorithm.
An experienced parallel programmer might immediately see this algorithm as an instance of one of our Partitioning patterns and could thus enter our pattern language at one of those patterns. Our pattern language, however, is targeted at professional programmers with little or no experience with parallel programming, and such programmers will need guidance from the pattern language to arrive at the right pattern.
(Space constraints make it impossible to give the full text of all patterns referenced. We refer interested readers to our pattern language in progress at http://www.cise.ufl.edu/research/ParallelPatterns/.)
The first step is to find the concurrency in the algorithm, using the FindingConcurrency design space. We first use the DecompositionStrategy pattern to help identify relatively independent actions in the problem (the tasks) and to define how data is shared or distributed between the tasks. This pattern and related patterns (TaskDecomposition and DataDecomposition) lead us to recognize that the major source of concurrency in our global optimization problem is the test-and-split-box calculations (i.e., computation of the interval extensions of the objective function for each of the boxes on the list), each of which can constitute a separate task. A second type of potentially concurrent task is the convergence test (the test of the list to see whether it meets the condition for ending the computation). The corresponding data decomposition is relatively straightforward: Each task operates almost exclusively on local data; the only shared data objects are the two lists of boxes (the input list and the results list).
The next step is to understand the dependencies between concurrent tasks, using the DependencyAnalysis pattern and its related patterns (GroupTasks, OrderTasks, and DataSharing).
For our global optimization problem, there are two well-defined groups of tasks: the tasks to perform the test-and-split-box computations (one per box), and the task to perform the convergence test.
Also, the order constraints between these groups are clear: The convergence test must wait until all the test-and-split-box computations have finished. These two task groups must therefore be executed in sequence (composed sequentially), giving us a computation consisting of two phases. Note also that the computation as a whole will likely consist of many iterations of first doing test-and-split-box calculations (computing interval extensions of the objective function for each box) and then checking for convergence, and these iterations also must be executed in sequence. At this point we do not need to decide exactly how we will meet these constraints; we just need to make a note of them and ensure that they are met as we proceed with the design.
Finally, we look at how data is shared between the two groups and within each group. The only data objects shared among tasks are the two lists of boxes. Because of the ordering constraint between the test-and-split-box tasks and the convergence-test task, we do not need to consider data sharing between these two groups of tasks but only among the tasks within each group. Each test-and-split-box task consists of removing one box from the input list, analyzing it, and possibly splitting it and putting the result(s) on the results list. Thus, we potentially have multiple tasks updating these shared data structures simultaneously, and we must be sure the algorithm we design ensures that concurrent updates do not produce wrong results. Again we do not have to decide at this point exactly how we will manage access to these shared data structures; we just need to note the data sharing and ensure that we handle it properly as we proceed.
The last stop in the FindingConcurrency design space is the CoordinationFramework pattern, which simply helps us review the design decisions made so far and be sure we are ready to move on to the next design space.
Most of the literature concerned with the use of patterns in software engineering associates code, or constructs that will directly map onto code, with each pattern. It is important to appreciate, however, that patterns solve problems, and that these problems are not always directly associated with code. Here, for example, the first set of patterns have not led to any code; instead they have helped the programmer reach an understanding of the best alternatives for structuring a solution to the problem. It is this guidance for the algorithm designer that is missing in most parallel programming environments.
At this point, we have determined what the concurrent tasks are, how they depend on each other, and what if any data must be shared between them; that is, we have "defined the exploitable concurrency". We are now ready to create a parallel algorithm that can use this concurrency to produce an effective parallel program, so the next step in the design process is to choose a high-level structure for the algorithm that organizes the concurrency, using the AlgorithmStructure design space.
In looking at what we know so far about our optimization problem, we see that the very top level of the algorithm can be structured as a sequential program -- a while loop with each iteration consisting of two phases, a test-and-split-boxes phase and a convergence-test phase (which includes copying the results list back to the input list). All the concurrency in our algorithm will occur during the first of these phases, so we use the patterns of the AlgorithmStructure space to design a structure for this phase.
Starting at the top of the decision tree in Figure 2, we choose the branch labeled OrderByTasks because overall a task-based decomposition seems to make the most sense. Note that an inexperienced parallel programmer might not make the best choice on the first pass through the decision tree; a designer may need several passes through the decision tree before an optimal design is produced. A systematic decision tree, however, provides a framework for designers to use in choosing a suitable algorithm structure.
Proceeding down the OrderByTasks branch, we must next decide whether the tasks in the first phase of our algorithm are organized linearly or recursively. When this phase of our algorithm begins, the size of the list of boxes is fixed, so we choose the Linear branch, which brings us to the Partitioning patterns. Next we consider dependencies among the tasks. Aside from their use of the input and results lists (and the input list is used only to be sure that each box is worked on exactly once), the tasks are completely independent. Therefore, we follow the Independent branch in the decision tree and arrive at our terminal pattern, the EmbarrassinglyParallel pattern.
We then read through the EmbarrassinglyParallel pattern (a copy of which appears as Appendix B), which guides us through the process of designing our parallel algorithm.
Mapping our problem onto the pattern, we see that the independent tasks of the pattern are our test-and-split-box tasks, the task queue is the input list of boxes, and the shared data structure to be used for storing results is the results list of boxes. Reviewing the Restrictions section of the EmbarrassinglyParallel pattern, we see that therefore we should implement both lists as "thread-safe" shared data structures. Once again, an experienced parallel programmer would know this right away, but someone with less experience with parallel programming would need to be guided to this conclusion.
At this point we have used our pattern language to decide the following:
We are now ready to start designing code.
As a first step in designing code, we consult the SharedQueue pattern. Ideally there would be a shared-queue library component that would provide exactly what is needed, a component that can be instantiated to provide a queue with elements of a user-provided abstract data type (in this case a box). If so, the pattern would explain how to use it; if not, the pattern would indicate how the needed shared data structure could be implemented.
We next consider program structure. Since the overall program is a sequential structure containing an instance of the EmbarrassinglyParallel pattern, it makes sense to use a fork-join structure (the ForkJoin pattern) for the test-and-split-boxes phase of the computation, with a master process setting up the problem, initializing the task queue, and then forking a number of processes or threads to perform the individual test-and-split-box calculations. Following the join, the master carries out the second phase of the computation: testing for convergence, copying the results list to the input list, and then (if necessary) repeating the whole two-phase cycle until the convergence condition is satisfied.
The following figure shows pseudocode for the resulting design. Note that although this pseudocode omits major portions of the program (for example, details of the interval global optimization algorithms), it includes everything relevant to the parallel structure of the program.
#define Nworkers N
SharedQueue<Interval_box> InList;
SharedQueue<Interval_box> ResultList;
void main()
{
int done = FALSE;
InList = Initialize();
While (!done) {
// Create Workers to test boxes on InList and write
// boxes that may have global minima to ResultList
Fork(Nworkers, worker);
// Wait for the join (i.e. until all workers are done)
Join();
// Test for completion and copy ResultList to InList
done = convergence_test(ResultList);
copy(ResultList, InList);
}
output(InList);
}
void worker ()
{
Interval_box B;
While (!empty(InList)) {
B = dequeue(InList);
// Use tests from Interval arithmetic to see
// if the box can contain minima. If so, split
// into sub-boxes and put them on the result list.
if (has_minima (B))
split_and_put (B, ResultList);
}
}
Figure 4: Pseudocode for the parallel global optimization program.
Having arrived at a design, we now consider how we would implement it in a particular programming environment, using the ImplementationMechanisms design space. We envision the programmer choosing a target programming environment and then using the Implementation sections of appropriate patterns to turn the pseudocode of the design into syntax for the chosen programming environment.
For example, consider how we would turn the pseudocode of Figure 4 into an OpenMP program, specifically how we would express the fork and join constructs in OpenMP. Recall that we chose these constructs to implement (in pseudocode) the ForkJoin pattern (in the SupportingStructures design space), so we would review the ForkJoin pattern to see how to produce the same result using OpenMP. The ForkJoin pattern would refer us to the Forall pattern in the ImplementationMechanisms design space, which in turn would tell us that it can be implemented using the OpenMP parallel for construct. The result would be the more OpenMP-specific pseudocode shown in Figure 5.
#define Nworkers N
SharedQueue<Interval_box> InList;
SharedQueue<Interval_box> ResultList;
void main()
{
int done = FALSE;
InList = Initialize();
While (!done) {
// Create Workers to test boxes on InList and write
// boxes that may have global minima to ResultList
#pragma omp parallel for
for(int i=0; i<Nworkers; i++)
worker();
// Test for completion and copy ResultList to InList
done = convergence_test(ResultList);
copy(ResultList, InList);
}
output(InList);
}
Figure 5: Pseudocode for the fork/join construct implemented with OpenMP.
Similarly, if there was no library component available for the SharedQueue pattern, the programmer would consult the Implementation section of the pattern for guidance on how to implement it for the desired environment. This section would guide the programmer into the ImplementationMechanisms design space.
In short, patterns in higher-level design spaces ultimately guide the programmer to patterns in the ImplementationMechanisms space. Patterns in this lowest-level space provide lower-level and programming-environment-specific help, such that after review of the relevant patterns in this space the programmer can finish the process of turning a problem description into finished code for the target environment.
In this paper, we described our ongoing research into the development of a pattern language for parallel application programming. Space constraints allowed us to provide only a limited view of our pattern language, consisting of a discussion of the design spaces used to organize the pattern language and a simple example of how these ideas would be used to design a parallel algorithm. In the appendices, we include a discussion of the notation used in the patterns and one of the patterns (the EmbarrassinglyParallel pattern).
While a complete presentation of our pattern language could not be included in this paper, we did provide enough information to understand the structure of the patterns themselves and how we are organizing them into a pattern language. This structure is not the only way to organize patterns into a pattern language, but after much experimentation, it is the most effective organization we have found.
To demonstrate how the patterns would be used in a design problem, we discussed a global optimization application. It is true that this is an embarrassingly parallel application and thus may appear trivial to parallelize. The need for organizing the tasks into two phases, however, was not obvious, nor was the need for use of a shared queue data structure. While we have not conducted tests with programmers inexperienced in parallel computing, we believe that our pattern language effectively exposed these issues and would have helped such a programmer develop a correct design. Clearly, we have more work to do in order to test this hypothesis.
As mentioned earlier, this is an ongoing project. It is also an ambitious project that will undergo considerable evolution as we complete more patterns and apply them to more applications. Interested readers can follow our progress towards a pattern language for parallel application programming at http://www.cise.ufl.edu/research/ParallelPatterns/.
We gratefully acknowledge financial support from Intel Corporation, the NSF, and the AFOSR.
[Chandy94] K.M. Chandy. "Concurrent program archetypes". In Proceedings of the Scalable Parallel Library Conference, 1994.
[Cole89] M.I. Cole. Algorithmic Skeletons: Structured Management of Parallel Computation. MIT Press, 1989.
[Coplien95] J.O. Coplien and D.C. Schmidt, editors. Pattern Languages of Program Design, pages 1--5. Addison-Wesley, 1995.
[Gamma95] E. Gamma, R. Helm, R. Johnson, and J. Vlissides. Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley, 1995.
[Massingill98] B.L. Massingill. "A structured approach to parallel programming", Technical Report CS-TR-98-04, California Institute of Technology, 1998 (Ph.D. thesis.). ftp://ftp.cs.caltech.edu/tr/cs-tr-98-04.ps.Z.
[Massingill96] B.L. Massingill and K.M. Chandy. "Parallel program archetypes". Technical Report CS-TR-96-28, California Institute of Technology, 1996. ftp://ftp.cs.caltech.edu/tr/cs-tr-96-28.ps.Z. Also to appear in Proceedings of the 13th International Parallel Processing Symposium and 10th Symposium on Parallel and Distributed Processing (IPPS/SPDP'99), 1999.
[Massingill99] B.L. Massingill, T.G. Mattson, and B.A. Sanders. "A pattern language for parallel application programming". http://www.cise.ufl.edu/research/ParallelPatterns/, 1999.
[MPI] "MPI: A message-passing interface standard". International Journal of Supercomputer Applications and High Performance Computing, 8 (3--4), 1994.
[Moore79] R.E. Moore. "Methods and Applications of Interval Analysis". SIAM, 1979.
[Moore92] R.E. Moore, E. Hanson, and A. Leclerc. "Rigorous methods for global optimization". In C.A. Foudas and P.M. Pardalos, editors, Recent Advances in Global Optimization, page 321, 1992.
[OpenMP] "The OpenMP standard for shared-memory parallel directives". http://www.openmp.org, 1998.
[Patterns98] "Patterns home page". http://hillside.net/patterns/patterns.html, 1998.
[Schmidt93] D.C. Schmidt. "The ADAPTIVE Communication Environment: An object-oriented network programming toolkit for developing communication software." http://www.cs.wustl.edu/~schmidt/ACE-papers.html, 1993.
We encode our patterns in a consistent format based on that of [Gamma95], with elements as described in this section. Not all patterns include all of these elements. When an element of the design pattern is not relevant, we just omit it from the pattern. We will ultimately present the whole collection of patterns making up our language in the form of a collection of Web-accessible documents connected by hyperlinks. See http://www.cise.ufl.edu/research/ParallelPatterns/ for the current version of this work in progress.
This section contains a brief statement of the problem solved by this pattern. The goal of this section is to make it easy for an application designer scanning through a number of patterns to decide quickly which pattern fits the problem to be solved.
This section lists other names by which a pattern is commonly known.
A pattern, recall, is defined as a "solution to a problem in a context". This section is where we describe the context in which one would use this pattern; it explains why a designer would use this pattern and what background information should be kept in mind when using it.
When writing down a pattern, one of the key goals is to give the application designer the information needed to quickly decide which patterns to use. This is so important that we do it in two sections, the Applicability section and the Restrictions section. The first (this section) discusses, at a high level, when the pattern can be used. The goal of this section is to help the designer decide whether the pattern really fits the problem to be solved.
In this section we provide details to help designers ensure that they are using the pattern safely. Ideally, if the restrictions are followed faithfully, the designer should feel confident that the use of this pattern will work. Thus, this section states restrictions carefully and completely, and it fully discusses unusual boundary conditions.
Where appropriate, this section contains a hyperlink to a Supporting Theory section. This supporting section provides a more rigorous theoretical justification for the guidelines to safe use of the pattern.
This section describes the components whose interaction defines the pattern; i.e., it looks "inside the box" of the pattern. These components can be other patterns in the language or more loosely-defined entities.
This section describes how the pattern works with other patterns to solve a larger problem; i.e., it looks "outside the box" of the pattern.
Every design decision has consequences; there are advantages and disadvantages associated with the use of any pattern. The designer must understand these issues and make tradeoffs between them. In this section, we give designers the information they need to make these tradeoffs intelligently.
This section explains how to implement the pattern, usually in terms of patterns from lower-level design spaces. The discussion focuses on high-level considerations common to all or most programming environments.
Programmers learn by example. In this section, we support this mode of learning by providing an implementation or implementations of the pattern in a particular programming environment. For patterns in higher-level design spaces, we often provide simply a pseudocode implementation; for patterns in lower-level design spaces, we provide sample code based on one or more popular programming environments such as OpenMP, MPI, or Java.
This section describes contexts in which the pattern has been used, where possible in the form of literature references.
This section lists patterns related to this pattern. In some cases, a small change in the parameters of the problem can mean that a different pattern is indicated; this section notes such cases.
In this section, we provide the complete text of one pattern. The other patterns in the language are available at http://www.cise.ufl.edu/research/ParallelPatterns/.
This pattern is used to describe concurrent execution by a collection of independent tasks. Parallel Algorithms that use this pattern are called embarrassingly parallel because once the tasks have been defined the potential concurrency is obvious.
Consider an algorithm that can be decomposed into many independent tasks. These embarrassingly parallel problems contain obvious concurrency that is trivial to exploit once these independent tasks have been defined. Nevertheless, while the source of the concurrency is obvious, taking advantage of it in a way that makes for efficient execution can be difficult.
The EmbarrassinglyParallel pattern shows how to organize such a collection of tasks so they execute efficiently. The challenge is to organize the computation so that all units of execution finish their work at about the same time -- that is, so that the computational load is balanced among processors.
This pattern automatically and dynamically balances the load. With this pattern, faster or less-loaded units of execution (UEs) automatically do more work. When the amount of work required for each task cannot be predicted ahead of time, this pattern produces a statistically optimal solution.
Use the EmbarrassinglyParallel pattern when:
The EmbarrassinglyParallel pattern is applicable when what we want to compute is a solution(P) such that
solution(P) =
f(subsolution(P, 0),
subsolution(P, 1), ...,
subsolution(P, N-1))
such that for i and j different, subsolution(P, i) does not depend on subsolution(P, j). That is, the original problem can be decomposed into a number of independent subproblems such that we can solve the whole problem by solving all of the subproblems and then combining the results. We could code a sequential solution thus:
Problem P;
Solution subsolutions[N];
Solution solution;
for (i = 0; i < N; i++) {
subsolutions[i] =
compute_subsolution(P, i);
}
solution =
compute_f(subsolutions);
If function compute_subsolution modifies only local variables, it is straightforward to show that the sequential composition implied by the for loop in the preceding program can be replaced by any combination of sequential and parallel composition without affecting the result. That is, we can partition the iterations of this loop among available UEs in whatever way we choose, so long as each is executed exactly once.
This is the EmbarrassinglyParallel pattern in its simplest form -- all the subproblems are defined before computation begins, and each subsolution is saved in a distinct variable (array element), so the computation of the subsolutions is completely independent.
There are also some variations on this basic theme.
One such variation differs from the simple form in that it accumulates subsolutions in a shared data structure such as a list or queue. Computation of subsolutions is no longer completely independent, but concurrency is still possible if the order in which subsolutions are added to the shared data structure does not affect the result.
For this and the simple form of the pattern, each computation of a subsolution becomes a "task" in the pattern (with care taken in the second case to use a thread-safe shared data structure), and the primary issues in producing a correct implementation are managing the task queue to be sure each task gets computed exactly once. (That is, the termination condition for the parallel part of the computation is that all tasks have been completed.)
Another variation differs from the simple form in that not all subproblems need to be solved. For example, if the whole problem consists of determining whether a large search space contains at least one thing meeting given search criteria, and each subproblem consists of searching a subspace (where the union of the subspaces is the whole space), then the computation can stop as soon as any subspace is found to contain something meeting the search criteria. As in the simple form of the pattern, each computation of a subsolution becomes a task, but now the termination condition is something other than "all tasks completed". This can also be made to work, although care must be taken to either ensure that the desired termination condition will actually occur or to make provision for the case in which all tasks are completed without reaching the desired condition.
A final and more complicated variation differs in that not all subproblems are known initially; that is, some subproblems are generated during solution of other subproblems. Again, each computation of a subsolution becomes a task, but now new tasks can be created "on the fly". This imposes additional requirements on the part of the program that keeps track of the subproblems and which of them have been solved, but these requirements can be met without too much trouble, for example by using a thread-safe shared task queue. The trickier problem is ensuring that the desired termination condition ("all tasks completed" or something else) will eventually be met.
What all of these variations have in common, however, is that they meet the pattern's key restriction: It must be possible to solve the subproblems into which we partition the original problem independently. Also, if the subsolution results are to be collected into a shared data structure, it must be the case that the order in which subsolutions are placed in this data structure does not affect the result of the computation.
Based on the preceding discussion, the keys to exploiting available concurrency while maintaining program correctness (for the problem in its simplest form) are as follows.
The variations mentioned earlier impose additional requirements:
The EmbarrassinglyParallel pattern views a computation as a collection of independent tasks. The structure of a program using this pattern includes the following three parts:
The EmbarrassinglyParallel pattern has some powerful benefits. First, parallel programs that use this pattern are among the simplest of all parallel programs. If the independent tasks correspond to individual loop iterations and these iterations do not share data dependencies, parallelization can be easily implemented with a parallel loop directive.
With some care on the part of the programmer, it is possible to implement programs with this pattern that automatically and dynamically adjust the load between processors. This makes the EmbarrassinglyParallel pattern popular for programs designed to run on parallel computers built from networks of workstations.
This pattern is particularly valuable when the effort required for each task varies significantly and unpredictably. It also works particularly well on heterogeneous networks, since faster or less-loaded processors naturally take on more of the work.
The downside, of course, is that the whole pattern breaks down when the tasks need to interact during their computation. This limits the number of applications where this pattern can be used.
There are many ways to implement this pattern. One of the most common is to collect the tasks into a queue (the task queue) shared among processes. This task queue can then be implemented using the SharedQueue pattern. The task queue, however, can also be represented by a simpler structure such as a shared counter, as in the SPMD example in the Examples section.
Frequently this pattern is implemented using two types of processes, master and worker. There is only one master process; it manages the computation by:
There can be many worker processes; each contains some type of loop that repeatedly:
Frequently the master and worker processes form an instance of the ForkJoin pattern, with the master process forking off a number of workers and waiting for them to complete.
A common variation is to use an SPMD program with a global counter to implement the task queue. This form of the pattern does not require an explicit master.
Termination can be implemented in a number of ways.
If the program is structured using the ForkJoin pattern, the workers can continue until the termination condition is reached, checking for an empty task queue (if the termination condition is "all tasks completed") or for some other desired condition. As each worker detects the appropriate condition, it terminates; when all have terminated, the master continues with any final combining of subsolution results.
Another approach is for the master or a worker to check for the desired termination condition and, when it is detected, create a "poison pill", a special task that tells all the other workers to terminate.
See the Restrictions section.
Consider a problem consisting of N independent tasks. Assume we can map each task onto a sequence of simple integers ranging from 0 to N-1. Further assume that the effort required by each task varies considerably and is unpredictable.
The following code uses the EmbarrassinglyParallel pattern to solve this problem. We implement the task queue as an instance of the SharedQueue pattern. To keep count of how many tasks have been completed we need a shared counter that can be safely accessed by multiple processes or threads, which we could implement as an instance of a SharedCounter pattern.
The master process, shown below, initializes the task queue and the counter. It then forks the worker threads and waits until the counter indicates that all the workers have finished. At that point it consumes all the results and then kills the workers.
#define Ntasks 500 /* Number of tasks */
#define Nworkers 5 /* Number of workers */
SharedQueue task_queue; /* task queue */
Results Global_results[Ntasks]; /* array to hold results */
SharedCounter done; /* count finished results*/
void master()
{
int Worker();
// Create and initialize shared data structures
task_queue = new SharedQueue();
for (int i = 0; i < N; i++)
enqueue(&task_queue, i);
done = new SharedCounter(0);
// Create Nworkers threads executing function Worker()
fork (Nworkers, Worker);
// Wait for all tasks to be complete; combine results
wait_on_counter_value (done, Ntasks);
Consume_the_results (Ntasks);
// Kill workers when done
kill(Nworkers);
}
The worker process, shown below, is simply an infinite loop. Every time through the loop, it grabs the next task, does the indicated work (storing the results into a global results array), and indicates completion of a result by incrementing the counter. The loop is terminated by the master process's killing the worker process.
int Worker()
{
int i;
Result res;
While (TRUE) {
i = dequeue(task_queue);
res = do_lots_of_work(i);
Global_results[i] = res;
increment_counter(done);
}
}
Note that we ensure safe access to key shared variables (the task queue and the counter) by implementing them using patterns from the SupportingStructures space. Note also that the overall organization of the master process is an instance of the ForkJoin pattern.
Another similar solution is the following, which explicitly uses a ForkJoin pattern to cause the master to wait until all workers have completed before proceeding.
#define Ntasks 500 /* Number of tasks */
#define Nworkers 5 /* Number of workers */
SharedQueue task_queue; /* task queue */
Results Global_results[Ntasks]; /* array to hold results */
void master()
{
int Worker();
// Create and initialize shared data structures
task_queue = new SharedQueue();
for (int i = 0; i < N; i++)
enqueue(&task_queue, i);
// Create Nworkers threads executing function Worker()
ForkJoin (Nworkers, Worker);
Consume_the_results (Ntasks);
}
void Worker()
{
int i;
Result res;
While (!empty(task_queue) {
i = dequeue(task_queue);
res = do_lots_of_work(i);
Global_results[i] = res;
}
}
As an example of implementing this pattern without a master process, consider the following sample code using the TCGMSG message-passing library. The library has a function called NEXTVAL that implements a global counter. An SPMD program could use this construct to create a task-queue program as shown below.
While (itask = NEXTVAL() < Number_of_tasks){
DO_WORK(itask);
}
There are many application areas in which this pattern is useful. Many ray-tracing codes use some form of partitioning with individual tasks corresponding to scan lines in the final image. Applications coded with the Linda coordination language are another rich source of examples of this pattern.
Parallel computational chemistry applications also make heavy use of this pattern. In the quantum chemistry code GAMESS, the loops over two electron integrals are parallelized with the TCGMSG task queue mechanism mentioned earlier. An early version of the Distance Geometry code, DGEOM, was parallelized with the Master-Worker form of the EmbarrassinglyParallel pattern. These examples are discussed in [Mattson94].
This pattern is closely related to the other Partitioning patterns, Reduction and SharedMemory.