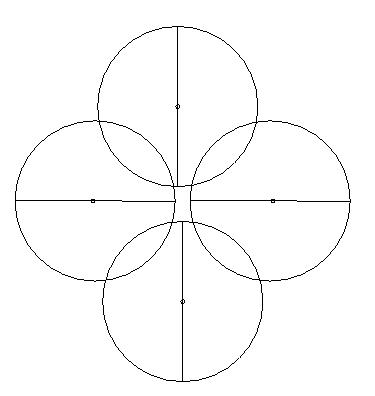
QUESTION: Would the scheme you suggested today (the old conflict rule) pick all four centers in the independent set?
If the answer is YES:
It should not because Ruppert's sequential algorithm would not. See the following picture for illustration of cyclic dependency. This is the same configuration as above, except I show the encroaching centers and their correspnding circles (dashed) as well.
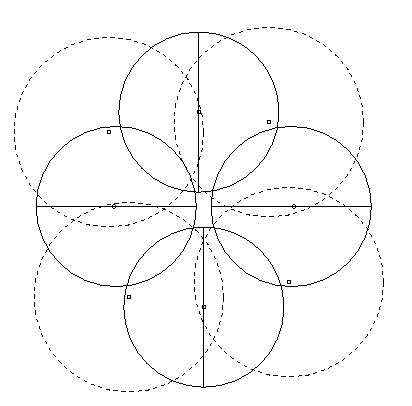
The dependency is CCW: each diametral center is waiting for the next encroaching circumcenter (CCW) and of course each circumcenter is waiting for the diametral center of the segment it is encroaching. This construction is similar to what I've sent you earlier, except I use only diametral circles and the corresponding encroaching circumcenters.
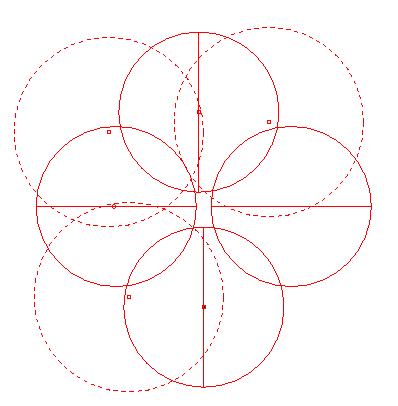
Say you inserted the diametral center of the edge in the bottom of the page.
That kills the circle on its right.
So there is nobody encroaching to the segment on the right.
So Ruppert's method would not split the segment on the right.
Yes, we can think of Ruppert's algorithm doing some redundant splits, but it does only when all the segments are encroached by the same circumcenter. It is not the case here.
If the answer is NO:
Can you quickly explain how the rule you suggested apply in this case?
Not being able to split the encroached segments is a problem
as we talked about today.
As an alternative to what you suggested (the old rule),
how about this one?
\begin{definition}
A circumcenter $\dot{c}_1$
and a diametral center $\dot{d}_1$
(and also the corresponding circles,
$c_1$ and $d_1$)
are said to be in {\em conflict} if
(i) $\dot{d}_1$ is inside $c_1$; and
(ii) $\dot{c}_1$ is not inside $c_1$; and
(iii) the radius of $c_1$ is smaller than $\sqrt{2}$ times the
radius of $d_1$.
Otherwise, $\dot{c}_1$ and $\dot{d}_1$ (also $c_1$ and $d_1$) are said to be
{\em independent}.
\end{definition}
Basically, I just added (iii) to the old rule which has (i) and (ii).
This rule is sufficient to realize the parallel output
with the sequential Ruppert.
In the picture, only the circumcircles whose center is inside the
the shaded area conflicts with a diametral circle.
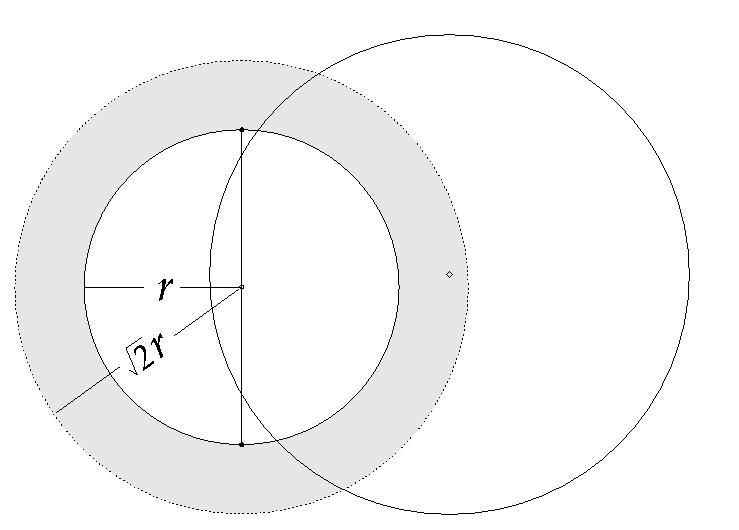
This way we do not eliminate large circumcircles that contains
center of a very small diametral circle.
