Data Structures, Algorithms, & Applications in Java
Chapter 12, Exercise 61
One way to generate a sequence of union and find operations is to
generate a sequence of n combine operations
(see page 245 of text). We use this strategy with m =
1.5 * n (this choice is rather arbitrary).
For n we use the values 1000, 2000,
4000, ..., 128000 (again, an arbitrary choice). For each
10
sequences of combine operations. For some n more than
10 sequences are used, because, for timing
accuracy reasons, we require that at least 1 second
be spent on each, code class=code>n.
The code for UnionFindWithTrees is given below.
To get the code for
FastUnionFind simply comment out the line
UnionFindWithTrees s = new UnionFindWithTrees(n[i]));
and uncomment the preceding line.
public class TimeUnionFind
{
public static void main(String [] args)
{
int [] n = {1000, 2000, 4000, 8000, 16000, 32000, 64000, 128000};
// number elements
int numberOfNs = 8;
int minSequences = 10; // average over at least this many sequences
int sequenceFactor = 5; // sequence length = sequenceFactor * n
for (int i = 0; i < numberOfNs; i++)
{// find average time for n[i] elements
int counter = 0; // number of sequences done so far
long startTime = System.currentTimeMillis();
int numberOfCombines = 5 * n[i];
Random r = new Random();
// use at least minSequences sequences of 5*n[i] combine operations
// also make sure at least 1 second has elapsed
while (counter < minSequences ||
System.currentTimeMillis() - startTime < 1000)
{
// initialize for n[i] elements
// FastUnionFind s = new FastUnionFind(n[i]);
UnionFindWithTrees s = new UnionFindWithTrees(n[i]);
// do the combine operations
for (int q = 0; q <= numberOfCombines; q++)
{
// select two elements at random
int u = r.nextInt(n[i]) + 1;
int v = r.nextInt(n[i]) + 1;
// do two find operations
int uSet = s.find(u);
int vSet = s.find(v);
// do a union only if uSet != vSet
if (uSet != vSet)
s.union(uSet, vSet);
}
counter++;
}
long timePerSequence = (System.currentTimeMillis() - startTime)
/ counter;
System.out.println("n = " + n[i] + " number of sequences = "
+ counter + " time/sequence = " +
timePerSequence + " ms");
}
}
}
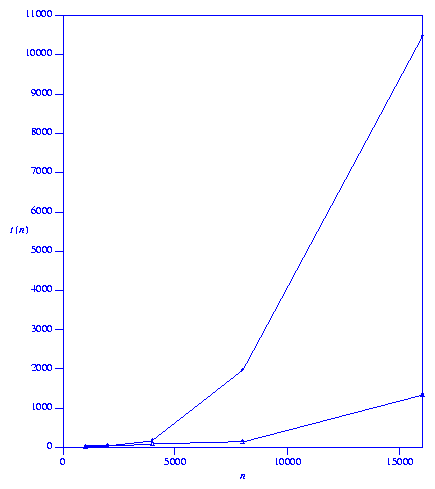
The measured times per sequence (in milliseconds) are given below.
``-'' indicates the time was not measured because it is too much.
| n |
UnionFindWithTrees |
FastUnionFind |
|
1000
|
14 |
5 |
|
2000
|
43 |
25 |
|
4000
|
176 |
73 |
|
8000
|
1966 |
137 |
|
16000
|
10485 |
165 |
|
32000
|
50378 |
258 |
|
64000
|
- |
626 |
|
128000
|
- |
1340 |
The times are plotted below. Bullets are used for UnionFindWithTrees
and deltas are used for FastUnionFind.