COT 3100 -- Discrete Structures: § 1: Introductory Material
Computer science is based on discrete mathematics, a relatively new
branch of mathematics. Discrete math emphasizes sets, and operations
over sets that are (or can be expressed in terms of) a subset of the
integers.
A key feature of modern computer science is the ability to specify the
functionality of computer programs in terms of mathematical
expressions. In order to exploit discrete mathematics, the computer
science student needs to learn how to read, understand, and manipulate
notation. In practice, such notation describes operands,
operations, algorithms, and analysis techniques
specific to computer related applications.
This section is organized as follows:
1.1. Introduction and Overview
1.2. Basic Concepts of Logic
1.3. Sets, Set Operations, Mappings, and Functions
1.4. Algorithms and Algorithmic Complexity
1.5. Integers, Matrices, and Number Theory
We begin with an overview of background and foundational material. To
establish proficiency, we will concentrate initially on learning
concepts and notation about logic, especially Boolean logic, or
operations over binary numbers (ones and zeroes). We then progress
to more general considerations of sets, operations over sets, maps,
and functions. We further generalize this information to include
algorithms and analysis of the computational complexity of algorithms.
Finally, we specialize our knowledge of number systems and functions
to discuss integers, modular arithmetic, matrices, and selected topics
from number theory.
1.1. Introduction and Overview
In order to set the proper context for this class, which is concerned
with high-level techniques that facilitate good algorithm and software
design, we begin with a discussion of software design and engineering
principles.
1.1.1. Software Design & Engineering Goals
Software design can be divided into two levels. High-level software
design and analysis seeks to produce correct, efficient
software. At a low level, one is more concerned with
robustness, adaptability, and reusability.
1.1.1.1. High-level Software Design Goals include:
- Correctness -- a data structure or algorithm is
designed, at a high level, to work as specified for all
possible inputs.
Example. A sorting algorithm must arrange
its inputs in ascending or descending order only.
- Efficiency implies (a) fast runtime, and (b) minimal
use of computational resources.
Example. Algorithm design for real-time systems
is not just a matter of using fast hardware. One must
produce fast algorithms that can take advantage of
commercial off-the-shelf (COTS) hardware, for decreased
production cost. Discrete math provides us with
techniques for evaluating the performance and
correctness of such systems.
1.1.1.2. Low-level Software Design Goals include:
- Robustness -- a program produces correct outputs
for all inputs on any hardware platform on which the
program is implemented. Robustness includes the
concept of scalability -- the capability of a
data structure or algorithm to handle expanding input
size without incurring prohibitive complexity or
causing inaccuracy or failure.
- Adaptability -- software must be able to be modified or
evolved over time to meet environmental changes
(e.g., increased CPU speed, client-server implementation,
or new functionality to increase market demand). Discrete
math can provide a rigorous framework for specifying new
software features.
Example. The Year 2000 Problem is an
excellent example of poor software design, where
date fields in old software (also called legacy
code) were not designed to be large enough to
accomodate date codes for an interval greater than
100 years. However, a cursory mathematical analysis
shows that the current 4-digit date format will only
be adequate to the year 10,000.
- Reusability -- a given partition or piece of code
must be able to be used as a component in different
systems or in different application domains without
significant modification.
Example. Upgrades to existing software
systems should be simple to design and implement,
but often aren't, due to idiosyncratic and poorly
engineered programming. Rigorous mathematical
analysis in terms of discrete mathematics theory
and techniques can help reduce some key design
errors, making software more reliable and portable.
The above-listed low-level goals are also covered in the CISE
Department's class entitled Data Structures and Algorithms
(COP3530). In this class, we will concern ourselves with the use of
high-level (mathematical) notation and techniques to describe the
functionality and analysis of algorithms, procedures, functions, and
operations that are typically encountered in digital computing.
Class #01: Wednesday 06 Jan 1999
1.1.2. Understanding Discrete Math
To meet the above-listed high-level goals, one must understand and be
able to manipulate expressions that contain operations
and operands. In most cases, such expressions are published in
research and development papers and reports as pseudocode,
which evolved from mathematical notation as computer science developed
since the 1940s.
Expressions include the following components:
- Operands that are typically expressed in terms of
sets, which are collections of elements.
Example. The zeroes and ones that comprise
machine language code are elements of the set of Boolean
numbers, denoted in this class as B = {0,1}. In
practice, Boolean numbers are operands of Boolean
logic functions.
- Operations that modify or combine set elements in
different ways, to produce a result that is typically input
to one or more additional operation.
Example. An operation such as the sine or
cosine function maps an element of the real numbers
R, within the principal value range of the function,
to a real-valued result.
- Quantifiers that tell the reader of a given expression
how the expression applies to its operands.
Example. Two kinds of quantifiers include
universal and existential operators. For
example, universal quantification says that a given
operation applies to all instances of a given
variable or variables. In contrast, existential
quantifiers merely express that there exists some instance
of a given variable that is input to a given operation, or
satisfies a given constraint.
1.1.3. Mathematical Foundations
Discrete math is based upon the following subdisciplines of mathematics:
- Measurement Theory -- Possibly the oldest branch of
mathematics, which provides information about the extent of
an object. For example, geometry probably evolved
from the science of measuring the earth -- first for
surveying land, then in support of astronomical
research related to navigation.
- Algebraic Manipulation provides rules and heuristics
for manipulation of mathematical symbols to obtain simpler
or more powerful expressions.
- Formal Logic provides operations and rules for solving
a broad range of problems that are centered mainly on the
Boolean logic. Other forms of logic (e.g., interval-valued
or "fuzzy" logic) exist, but have been developed
recently. Thus, the rules for manipulating such logics in
an effective way are still evolving.
In each of the episodes of discovery and learning that we embark upon
in this class, we will be emphasizing primarily manipulation of
operations in support of the instance of formal logic called Boolean
logic.
1.1.4. Additional Concepts
Discrete math is also based upon two concepts derived from sampling
theory, namely:
- Quantization -- when a continuous function is
sampled across its domain or range, so as to
produce a finite set of domain or range values, we
say that the continuous domain has been quantized
or sampled, and likewise for the range.
- Continuity Assumption supports the feasibility of
quantizing continuous functions. In a colloquial sort of
way, one assumes that, given a sufficiently small sampling
interval, the quantization of a continuous function
f yields a discrete approximation to f within
a prespecified error. This error limit is chosen to
support levels of accuracy and precision that render the
quantized (discrete) operation which portrays f
robust for a given set of operational constraints.
1.2. Basic Concepts of Logic
We begin our summary exposition of discrete mathematics with a
discussion of Boolean numbers.
1.2.1. Boolean Number System and Boolean Operations.
Concept. Western thought historically tends to emphasize
binary classification problems (e.g., good/bad, true/false, etc.),
which have until recently colored much Western thought. It is not
surprising, therefore, that logicians in the nineteenth century
(and before) sought a way to describe mathematical statements as
true or false, correct or incorrect.
High-Level Representation. Boolean logic uses 0 to represent the
value false and 1 to represent the value true.
Low-Level Representation. The Boolean numbers B = {0,1}.
Example. Suppose that today is Wednesday. Then,
- The predicate
(today = Thursday) is false,
i.e., we write (today = Thursday) = 0.
- In contrast, the predicate
(today =
Wednesday) = 1, given the preceding assumption.
Applications. Boolean logic is used throughout digital
computing, including hardware and software design, logical analysis
of languages, and design/analysis of algorithms.
In order to manipulate Boolean numbers in a useful way, we need to
define some operations over B.
Concept. A binary operation accepts two inputs
(or arguments) and produces a result. A unary operation
accepts one input and produces a result. Boolean logic contains both
unary and binary operations.
High-Level Representation. Boolean logic has as its basic
operations the unary operation of negation (denoted by
not), and the binary operations of and, or,
and xor. Note that xor is properly called
exclusive-or, whereas the or operation is properly
called inclusive-or.
Low-Level Representation. A unary operation on the Boolean
numbers can be denoted by f1 : B ->
B, whereas a binary Boolean operation can be denoted by
f2 : B × B -> B.
Boolean operations are defined in terms of truth tables,
which describe the results obtained from various combinations of
input values.
Examples. The following truth tables pertain to our discussion:
x x
not(x) | 0 1 and(x,y) | 0 1
-------+------- ---------+-------
| 1 0 0 | 0 0
y |
1 | 0 1
x x
or(x,y) | 0 1 xor(x,y) | 0 1
---------+------- ---------+-------
0 | 0 1 0 | 0 1
y | y |
1 | 1 1 1 | 1 0
Applications. All digital computation can be performed in
terms of the preceding Boolean operations. In fact, it has been
shown that all digital computation can be performed in terms of
the nand(x,y) = not(and(x,y)) operation! We
will discuss this concept when we discuss Chapter 9 of the text
(Rosen, Discrete Math and its Applications, 4th Ed.), which
pertains to digital logic.
Exercises.
(1) Build a truth table for the following function:
f(x,y) = not(x and y) and x .
(2) Question: If a Boolean function has n input variables,
then how many entries are there in the truth table?
Hint: Formulate a Boolean function with variables x, y, and
z, as well as w, x, y, and z. Count the number of different
combinations for each case, and discover what trend
emerges.
Class #02: Friday 08 Jan 1999
1.2.2. Elements of Logical Discourse.
We next continue with the concepts of propositions (Section
1.2.2.1), implications (Section 1.2.2.2), and rules for
manipulating logical statements (Section 1.2.2.3).
1.2.2.1. Propositions are important concepts in the
formulation of precise, concise logical discourse (a collection
of statements that are grounded in formal logic).
Concept. The rules of logic constrain mathematical
statements to be (a) precise and (b) concise. Propositions
are sentences in the language of mathematics.
Background. Mathematical textbooks were often difficult to
understand or interpret prior to the 19th century, due to
the use of natural language (the vocabulary and
grammar used in everyday speech). The presentations of
concepts, ideas, theorems, etc. were often ambiguous and
profuse instead of being precise and concise. To remedy
this situation, many mathematicians (among them, George
Boole) contributed to the development of symbolic
logic (also called formal logic) to achieve
precision and concision in mathematical statements.
Definition. A proposition is a statement that is
either true or false, but not both.
Example 1. Hillary Clinton is President of the USA
[false] .
Example 2. 1 + 1 = 2 [true] .
Example 3. If today is
Wednesday, then it is raining [truth depends on the day] .
High-Level Representation. Given Boolean variables
x,y,z  B
let z = P(x,y), where P(x,y) denotes a
proposition.
B
let z = P(x,y), where P(x,y) denotes a
proposition.
Low-Level Representation. Propositions are comprised
of (a) operations such as the Boolean logic functions
and, or, and not, and operands
that are constants, variables, predicates, or propositions
which evaluate to a Boolean value (e.g., a zero or one).
Example 4. z = x or y, where x,y
 B.
B.
Note. Propositions can be tested exhaustively
with truth tables, and analytically with rules for
manipulating logical statements (Section 1.2.2.3).
Applications. Language translation has been a goal of
the subdiscipline of computer science called Artificial
Intelligence. In order to translate statements from one
natural language (NL) into another, we need to first determine
the structure of the source NL statement.
For example, the statement It is not the case that
today is Tuesday and it is raining could be translated
into logical form as:
not[(today = Tuesday) and
(weather = rain)]
One of the problems of language translation is that
humans cannot necessarily agree on what a sentence means.
For example, Time flies like an arrow could mean that
(a) time moves along in linear fashion, or (b) there are
insects called time flies who are fond of arrows.
What other meanings can you infer from the preceding
sentence?
Due to the inherent ambiguities in NL translation, we
will not spend much time on these applications, preferring
to concentrate instead upon the understanding, manipulation,
and verification of statements in logical form. Thus, we
continue with the concept of logical implication.
1.2.2.2. Logical Implications are represented by constructs
such as the if...then... construct in the sentence If today
is Tuesday, then it must be raining.
Concept. Western thought in particular, and human
thought in general, makes much of the concept of
causality. We tend to say things like if Princess
Diana's car had not gone through the tunnel at 100mph, she
might still be alive today. Here, we are implying that
going through a particular tunnel at 100mph was the cause of
the automobile crash where Princess Di met her end. Hence,
such implication expresses conditional
relationships that tend to be interpreted causally in
the context of natural discourse. That is, if we write
x -> y (read: x implies y or if x,
then y), this could be correctly or incorrectly
interpreted in terms of natural language as x causes y to
occur.
Caution. In this class, we are studying formal
logic, which is in the realm of formal discourse,
not natural language. Thus, one should not try to
relate the concepts of truth or falsity, condition or
causality, to one's emotions, feelings about values or
principles, or the passing scene of everyday life. This
statement is not meant to discourage one from studying or
contemplating such topics. However, for the purposes of
this class we note that formal logic is a self-contained
sub-discipline of mathematics that has its own rules for
notation and manipulation. Thus, it behooves one to learn
these rules and apply them in the context for which they are
intended, namely, mathematics. This can be done without
introducing concepts or values outside the realm of
mathematics, which tend to induce ambiguity into logical
discourse.
Representation. Let p and q denote propositions. The
following implications are employed in logical discourse:
- The conditional implication p -> q
reads "p implies q", "if p, then q", "q if p", "p only if
q", "q is necessary for p", "p is sufficient for q", or "q
whenever p", and has the following truth table:
p
p -> q | 0 1
---------+-------
0 | 1 0
q |
1 | 1 1
- The biconditional implication p <-> q
reads "p is necessary and sufficient for q", "p if and
only if q", "p iff q", "if p, then q, and conversely",
and has the following truth table:
p
p <-> q | 0 1
---------+-------
0 | 1 0
q |
1 | 0 1
Note that this truth table has the same form as the
truth table for the xnor = not(xor)
function described in the preceding section.
We next discuss the concept of propositional equivalence,
in the definition of which the biconditional implication is employed,
as shown in red typeface below.
Concept. Two propositions are said to be equivalent
if and only if they evaluate to the same Boolean values for
all inputs.
Definition. Given x1, x2, ...,
xn  B,
two propositions
p(x1,x2,...,xn) and
q(x1,x2,...,xn) are
said to be equivalent if and only if
they evaluate to the same Boolean values, which we
write mathematically as
B,
two propositions
p(x1,x2,...,xn) and
q(x1,x2,...,xn) are
said to be equivalent if and only if
they evaluate to the same Boolean values, which we
write mathematically as
p  q <->
p(x1,x2,...,xn)
= q(x1,x2,...,xn) ,
q <->
p(x1,x2,...,xn)
= q(x1,x2,...,xn) ,
 x1, x2, ...,
xn
x1, x2, ...,
xn  B .
B .
Example. The propositional equivalence p ->
q  not(p) or q is proven via a truth table,
as follows:
not(p) or q is proven via a truth table,
as follows:
+---+---+--------+--------+--------------+
| p | q | not(p) | p -> q | not(p) or q |
+---+---+--------+--------+--------------+
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
+---+---+--------+--------+--------------+
1.2.2.3. Rules for Manipulating Logical Statements are the
"bread and butter" of applications such as theorem proving.
Recall that the number of entries (rows) in a truth table varies as
2n, where n denotes the number of logical variables. (In
the preceding example, there were two variables, p and
q.) Proof by exhaustion (using complete truth tables) can become
prohibitively costly for large expressions involving many variables.
We remedy this situation with rules for manipulating logical
statements, which we outline as follows, and which are stated in the
text (Rosen, Discrete Mathematics and its Applications, 4th
Edition) in Table 5 (page 17).
Assumption. Let p,q,r  B and x,y,z
B and x,y,z  R.
This assumption will hold for the subsequent discussion.
R.
This assumption will hold for the subsequent discussion.
Identity. In arithmetic with real numbers, x · 1 = x
and x + 0 = x. In logic, the analogous statements are
p and 1  p,
and p or 0
p,
and p or 0  p .
p .
Domination. In arithmetic with real numbers, x · 0 = 0.
The logical analogue is
p and 0  0 .
0 .
Symmetrically, p or 1
 1 .
1 .
Idempotency. This property can be used to simplify
and or or operations, i.e.,
p or p  p
p
p and p  p .
p .
Double Negation. In arithmetic, -(-x) = x. In logic,
not(not(p))  p.
p.
Commutativity. In arithmetic, addition and multiplication
are commutative, i.e., x + y = y + x and x · y = y · x.
In logic, we have analogous formulations:
p or q  q or p
q or p
p and q  q and p .
q and p .
Associativity. In arithmetic, addition and multiplication
are associative, i.e., (x + y)+ z = x + (y + z) and (x ·
y) · z = x · (y · z). In logic, we have the
analogous formulations:
(p or q) or r  p or (q or r)
p or (q or r)
(p and q) and r  p and (q and r) .
p and (q and r) .
Distributivity. In arithmetic, multiplication distributes
over addition. In logic, we have a similar situation:
p and (q or r)  (p and q) or (p and r)
(p and q) or (p and r)
p or (q and r)  (p or q) and (p or r) .
(p or q) and (p or r) .
DeMorgan's Laws. Manipulation of logical statements is
greatly aided by DeMorgan's laws, which describe a property
that resembles distributivity:
not(p or q)  not(p) and not(q)
not(p) and not(q)
not(p and q)  not(p) or not(q) .
not(p) or not(q) .
Several other useful equivalences include:
- p or not(p)
 1
1
- p and not(p)
 0
0
- p -> q
 not(p) and q
not(p) and q
Exercises. Build truth tables for (a) distributive and (b)
DeMorgan's Laws, listed above.
Class #03: Monday 11 Jan 1999
In the preceding lecture, we discussed logical operations on
propositions, called implications and equivalences. In
this lecture, we will explore the concepts of relations,
predicates and quantifiers.
1.2.2.4. Relations and Predicates. Predicates are formed
from relations, which associate two objects in a specific way.
Concept. Relations provide a way of comparing
mathematical objects that can yield a Boolean value. For
example, one can compare the size of two real numbers x and y using
a construct such as (x < y), and obtain the Boolean constant
true (if x < y) or false (if x  y). This technique allows us to treat the
evaluated relation as a Boolean variable, from which one or
more propositions can be constructed.
y). This technique allows us to treat the
evaluated relation as a Boolean variable, from which one or
more propositions can be constructed.
Definition. An F-valued relation R on set
S is denoted by the mapping R : S × S -> F.
This means that R accepts two arguments, each of which
is an element of a set S, and produces a result that is an
element of set F.
Note: The symbol "->" in the preceding definition is
not the conditional implication operation, but refers to
a mapping between the domain of the map (on the
left-hand side of "->") and the range of the map
(on the right-hand side of "->").
Example. A computer implementation of the relation > :
R × R -> B (1) accepts two real
numbers x and y, (2) compares them, and (3) outputs
true if x > y, or false otherwise.
Definition. A predicate P is a Boolean-valued
relation on a set S, i.e., P : S × S -> B.
Example. In the preceding example, the predicate
corresponding to the relation ">" would be written (x > y).
Example. Predicates can be used to construct propositions
such as (x < y) or (x = y), which can be condensed
to yield (x  y).
y).
1.2.2.5. Quantifiers. Another important class of mathematical
objects is called quantifiers, of which there are two
instances, namely, the universal and existential quantifiers.
Concept. Quantifers help establish the universe of
discourse over which a proposition is defined. This
supports precision in logical expression.
Background. The developers of the formal logic understood
that some logical statements are valid over a large set of
conditions, constraints, or inputs. Other statements are
valid only for special, highly restricted cases. Additionally,
there may be exceptions to certain statements. Quantifiers
help express such situations.
Low-Level Representation. Two quantifiers will be employed,
which are:
- Existential Quantifier, denoted by
 , where
, where  (x) P(x) means there
exists some x such that P(x) holds.
(x) P(x) means there
exists some x such that P(x) holds.
- Universal Quantifier, denoted by
 , where
, where  (x) P(x) means that
for all x P(x) holds.
(x) P(x) means that
for all x P(x) holds.
Observation. Just as there were equivalences among
logical propositions, so there are equivalences among
quantifiers, for example,
not (x) P(x)
(x) P(x) 
 (x) not(P(x))
(x) not(P(x))
not (x) P(x)
(x) P(x) 
 (x) not(P(x))
(x) not(P(x))
Given these theoretical and manipulative tools, we are ready to
address concepts of sets and mappings.
Class #04: Wednesday 13 Jan 1999
1.3. Sets, Set Operations, Mappings, and Functions
In the preceding classes, we touched upon concepts of sets,
by talking about Boolean numbers B = {0,1}, the set
contains zero and one. We also mentioned a universe of discourse
that could be defined by quantifiers. In this class, we discuss
in greater detail the concepts of sets and operations over sets.
1.3.1. Sets and Set Operations
The concept of a set is basic to mathematics, and is (as we shall
see in the following discussion) an axiomatic concept in
mathematics.
Definition. A set is an abstraction that describes
a collection of elements.
Example. The real numbers are a collection of numbers,
each of which have a whole part followed by a decimal part (e.g.,
123.4567...)
Background. Sets are the building blocks of
higher-level formalisms that describe mappings and functions,
from which computer-language procedures, functional
constructs, and subroutines are derived.
Definition. Objects in a set are called members
or elements of a set.
Observation. Note that we do not define a set in terms of
some lower-level construct. For example, we do not say that
a set is a collection of elements of arbitrary type. In
that case, a set element could be the set itself. This
leads to Cantor's paradox, which is based on the
concept that a set should not contain itself. Hence, we simply
accept the existence of something called a set that is a
collection of elements. This is called an axiomatic
concept, namely, an object that is assumed to exist and
cannot be further defined without raising troublesome
inconsistencies or circular definitions.
Exercise. What other axiomatic concepts can you think of?
What inconsistencies do these axioms help circumvent?
Definition. Two sets are equal if and only if they
have the same elements.
Example. Let set A = {1,2,3} and set B = {3,1,2}.
Then A = B, since the A and B have the same elements.
Now that we have established what a set is, let us define some
ways of describing sets.
Concept. It is useful to describe sets in terms of
equations or expressions that generate elements of a
set. In computer science, such expressions can often
be implemented as algorithms, or recipes for computation.
Set-Builder Notation. We define sets in terms of the
following type of expression:
set-name = { element-name :
element-definition , constraint(s) }
which is called set-builder notation.
Example. The integers modulo n are defined as:
Zn =
{ x :
0  x
x  n-1 ,
x
n-1 ,
x  Z }
Z }
where the set-builder notation is comprised of the following:
- set-name is given as "Zn" ;
- the symbol "=" shows that the set definition follows ;
- the open brace "{" denotes the beginning of the
set definition .
- element-name is given as "x" ;
- the symbol ":" is part of the set-element's definition
and means such that ;
- element-definition is given by the expression
0
 x
x  n-1 ;
n-1 ;
- constraint is given by x
 Z , so x is not
mistaken for a real number ; and
Z , so x is not
mistaken for a real number ; and
- the closed brace "}" denotes the end of the set
definition .
In certain cases, one or more of the constraints can be
grouped with the element-name part of the definition,
for example,
Zn =
{ x  Z :
0
Z :
0  x
x  n-1
} ,
n-1
} ,
which increases the conciseness of the definition without
sacrificing accuracy. However, we would not want to
write:
Zn =
{ 0  x
x  n-1 :
x
n-1 :
x  Z }
Z }
which is poor style (element-definition munged into
the element-name). As in all linguistic expression,
a good sense of style is only gained by reading many
different (mathematics) texts and (research) papers, and
practicing writing such expressions, keeping the goals of
precision, concision, and clarity
uppermost in your mind.
Concept. Although set-builder notation is useful mathematically,
it is also useful to visualize sets and relationships
between sets using a construct known as Venn diagrams.
High-Level Representation. A Venn diagram is comprised of
the following elements:
- A bounding box that represents the universe of
discourse, usually denoted by U ;
- One or more circles or closed curvilinear figures,
each of which represents a set and is usually labelled
with a symbol such as A or B;
- [Optional] Shaded areas inside the set representations
that represent special properties of one or more sets;
- [Optional] Points or symbols inside the box or
set representations that represent elements of one or
more sets; and
- [Optional] Straight or curved arrows drawn from
one set to another, or between set element representations,
that themselves represent mappings or instances of mappings.
Example. Figure 1.1 illustrates two Venn diagrams, one of
disjoint sets A and B (having no elements in common), and
another of conjoint sets A and B (having some but not all
elements in common). The common elements of conjoint sets
comprise the intersection of such sets.

Figure 1.1. Venn diagrams of sets (a) that have
no members in common, and (b) have some but not all
members in common, (c) that have all members of one
set (but not all members of the other) in common.
Given the preceding theoretical and visualization tools, we can now
define some common set operations.
Concept. Sets can be arranged hierarchically, since they
can contain other sets (but not themselves) and also can
have elements that are not sets. The relations of
membership, subset and the power set
operator comprise the means by which hierarchical
relationships between sets can be described.
Definition. If x is an element (or member) of set S,
we write x  S. If x is
not in S, we write x
S. If x is
not in S, we write x 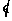 S.
S.
Definition. The null set or empty set has no
elements, and is denoted by ø.
Definition. A subset A of a set B has as its elements
some (proper subset) or all (improper subset) of the elements
of B. If A is a proper subset of B, then we have the
mathematical expression of this definition as
A  B
<-> A = {x : x
B
<-> A = {x : x  B } .
B } .
The Venn diagram representation for A  B is shown in Figure 1.1(c).
B is shown in Figure 1.1(c).
Example. If B = {1,2,3}, then A = {1,2} is a subset of
B, but C = {3,4} is not a subset of B, because B does not
contain the element "4".
Definition. The power set of A, denoted by 2A,
contains all possible subsets of A.
Example. If A = {a,b}, then 2A = {{a},{b},{a,b},
ø}. Note that the power set
contains the empty or null set.
Definition. The cardinality of a set S is the number
of elements in that set, denoted by |S|.
Example. If A = {a,g,d}, then |A| = 3.
Observation. If there are n elements in set A, then the
power set of A contains 2n elements. That is, if
n = |A|, then
|2A| = 2|A| = 2n .
Example. Note that 2ø
= {ø}, and
2{ø}
= {ø, {ø}}.
Thus, |2ø| = 1 and
|2{ø}| = 2.
Definition. The Cartesian product of two sets A and B
is a set of ordered pairs, where the first element of each
pair is an element of A, and the second element of each pair
is an element of B. The Cartesian product of A and B is written as
A × B = {(x,y) : x
 A and y
A and y
 B } .
B } .
Example. If A = {1,2} and B = {a,b}, then A × B =
{(1,a),(2,a),(1,b),(2,b)}.
Observation. The cardinality of the Cartesian product
is the product of the cardinalities of the constituent sets, i.e.,
|A × B| = |A| · |B| .
Example. In the preceding example, |A| = |B| = 2, and
|A × B| = |A| · |B| = 2(2) = 4.
Definition. The union of two sets A and B is
given by
A 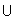 B
= {x : x
B
= {x : x  A or x
A or x
 B } .
B } .
Definition. The intersection of two sets A and B is
given by
A 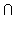 B
= {x : x
B
= {x : x  A and x
A and x
 B } .
B } .
Example. Let A = {1,2,3} and B = {2,3,4}. Observe that A
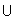 B = {1,2,3,4}, i.e.,
all elements in A or in B, while A
B = {1,2,3,4}, i.e.,
all elements in A or in B, while A 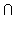 B = {2,3}, i.e., all elements
common to both A and B.
B = {2,3}, i.e., all elements
common to both A and B.
Definition. If A 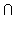 B = ø, then A and B are said to be
disjoint sets or disjunct sets. This
situation is illustrated in Figure 1.1(a). If A and B are
not disjoint, then they are conjoint or conjunct.
B = ø, then A and B are said to be
disjoint sets or disjunct sets. This
situation is illustrated in Figure 1.1(a). If A and B are
not disjoint, then they are conjoint or conjunct.
Concept. It is useful to be able to remove elements from
sets. This operation is called set subtraction.
Definition. If A and B are conjoint sets, then set
subtraction of B from A, denoted by A\B or A - B, is
given by
A \ B = {x : x  A and x
A and x 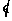 B} .
B} .
It follows that, if A and B are disjoint, then A \ B = A.
The Venn diagram for set subtraction is shown in Figure 1.2(a).
Example. If A = {1,2,3,4} and B = {3,4,5,6}, then
A \ B = {1,2}, since 1 and 2 are in A and 1 and 2
are not in B.
Exercise. Note that |A \ B| = |A| - |A 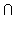 B|. Why is this so?
B|. Why is this so?
Definition. Given a universe of discourse U
of which a set A is a subset, the complement of A with
respect to U, denoted by A', is given by:
A' = U \ A .
Note that the complement may also be written with a horizontal
bar over the set name. The Venn diagram for set complement
is shown in Figure 1.2.

Figure
1.2. Venn diagrams for (a) set subtraction, and (b) set
complement.
Observation Set identities enable us to manipulate sets
analogous to the manipulation of logic operations, as
discussed in Section 1.2.2.3, above. Since the set
identities are analogous to the logical identities, we do
not reproduce them here, but refer the reader to Table 1 on
page 49 of the text (Rosen, Discrete Mathematics and its
Applications, 4th Edition).
We next consider an application for set notation and representations
such as the Venn diagram, namely, the specification of mappings.
Class #05: Friday 15 Jan 1999
1.3.2. Mappings
Mappings are of interest in mathematics since they provide a
high-level formalism for describing operations, a special case of
which are functions.
Concept. A mapping provides a way to assign
values in one set to values in another set.
Background. The type of assignment or association
represented by a mapping is foundational to mathematics and
computer science. For example, programming language
constructs such as functions, procedures, and subroutines,
can map a set of input parameters to one or more output
data.
High-Level Representation. As shown in Figure 1.3, there
are two considerations when dealing with a mapping, namely,
(1) arity and (2) coverage. Each instance of
a mapping can map m set elements to k set elements, where k
and m denote integers greater than zero. Thus, we have
mappings with 1-to-1 arity, m-to-1 arity, m-to-k arity
(where m,k > 1), and 1-to-k arity, as shown in Figures
1.3a-c, respectively. We also have coverage that is called
into or onto, as shown in Figures 1.3e and
1.3f, respectively. Note that a mapping has both
arity and coverage, so a 1-to-1 and onto mapping
is a valid mathematical object.

Figure
1.3. Mappings that are (a) 1-to-1, (b) m-to-1, (c) m-to-k,
(d) 1-to-k, (e) into, and (f) onto.
Low-Level Representation. A mapping M :
A -> B is represented as the set
M = {(x,y) :
x  A and
y
A and
y  B }
B }
which is a subset of the Cartesian product A × B. A is
called the domain of M, written
domain(M) and A is called the range of
M, written range(M).
Definition. An m-to-1 mapping M associates one or
more than one element in domain(M) with each
element in range(M).
Definition. A 1-to-1 mapping M associates each
element of domain(M) with one and only one
element in range(M).
Definition. An into mapping M : A -> B
does not associate elements of A with all elements of B.
Definition. An onto mapping M : A -> B
associates elements of A with all elements of B.
Example. The map M that associates each letter of
the English alphabet with an integer that describes the
position of that letter in its alphabet is written in set
notation as M = {(a,1), (b,2),...,(z,26)}. This map
is one-to-one and onto.
1.3.3. Functions
A special type of mapping that is employed in a wide variety of
mathematical applications is called a function. This term
has a precise mathematical meaning, as shown below.
Definition. A function is an m-to-1 and
onto mapping.
Definition. If f is a function from A to B
(i.e., f : A -> B), then A is called the domain
of f and B is called the co-domain of f .
Definition. A function is injective if it is a
1-to-1 mapping.
Definition. A function is surjective if it is an
onto mapping.
Definition. A function is a bijection if it is a
1-to-1 and onto mapping.
Example. If A = {1,2,3}, B = {a,b,c}, and M : A -> B, then
- M = {(1,a),(1,b),(2,b),(3,c)} is a surjection.
- M = {(1,a),(3,c)} is an injection.
- M = {(1,a),(3,b),(2,c)} is a bijection.
1.3.3.1. Composition of Functions. It is often useful to
combine functions to produce other functions. Chaining functions
(say, f and g) together (as in f(g(x)) )
is an important strategy in many types of computations, including
signal and image processing. This strategy is described
mathematically in terms of composition of functions.
Definition. If f : A -> B and g : B -> C
are functions, then the composition of f and g,
denoted by f o g, is defined as
f o g = {(x,y)
: y = g(f(x)), x  A}
A}
Example. Let f = {(1,a),(2,c),(3,b)} and
g = {(a,#),(b,%),(c,@)}. Then,
f o g = {(1,#),(2,@),(3,%)}.
Observation. In the preceding definition and example, the
functions f and g can be composed because
domain(g) = range(f). However,
the composition g o f is not
valid in this case, since domain(f)
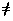 range(g). This is illustrated in the
diagram of Figure 1.4, which illustrates functional
composition graphically.
range(g). This is illustrated in the
diagram of Figure 1.4, which illustrates functional
composition graphically.
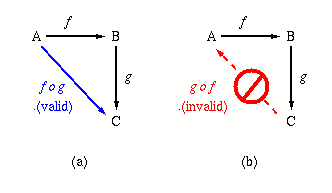
Figure 1.4. Graphical illustration of composition of
functions f : A -> B and g : B -> C , showing
(a) valid composition f o g and
(b) invalid composition g o f.
Remark. Composition of functions has numerous
applications, for example, in the formulation of
polynomials, as shown in the following definition.
Definition. If f,g : A -> R,
then f + g and f · g
are also functions from A to R, which are
given by
(f + g)(x) =
f(x) + g(x) , and
(f · g)(x) =
f(x) · g(x) ,  x
x  A .
A .
Example. Let f(x) = x2 and
g(x) = x3. Then,
(f + g)(x) =
x2 + x3 , and
(f · g)(x) =
x2 · x3 = x5 .
1.3.3.2. Inverse Functions. Another important concept
in the study of mappings and functions is inverse functions, which are
employed in the solution of equations.
Concept. Sometimes we want to reverse (or invert)
the order of sets in a mapping (e.g., from B to A instead
of from A to B).
Background and Application. The most common application of
inverse functions is solving systems of equations. For
example, if one has a physical model of an image formation
process, then it can be useful to invert the model (if
possible) to find out what input parameters result from
various outputs. This technique can be used in
model-based object recognition, an important task in
a subdiscipline of Artificial Intelligence called image
understanding.
Definition. If f : A -> B is 1-to-1, then
f has an inverse denoted by f-1 : B
-> A. This is shown by red arrows in Figure 1.5(a). If
f is into, then f-1 will
be onto. Otherwise, if f is onto,
then f-1 will be onto.
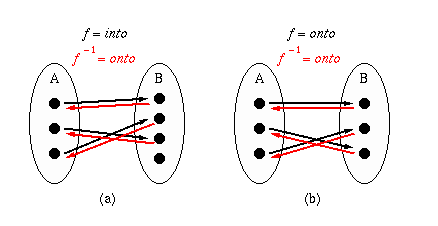
Figure 1.5. Graphical illustration of functional inversion,
where f is (a) into or (b) onto.
Example. If the function f = {(1,a),(2,c),(3,b)},
then f-1 = {(a,1),(c,2),(b,3)}.
Exercise. What kinds of mappings are invertible?
What kinds of mappings are not invertible? Why?
1.3.3.3. Useful Functions. Two important functions in
computer science are the ceiling and floor functions,
defined as follows.
Definition. The ceiling function, written ceiling(x)
or ceil(x) or 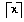 , is
defined as the smallest integer greater than or equal
to x.
, is
defined as the smallest integer greater than or equal
to x.
Examples. (1) If x = 3.0, then 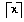 = 3. (2) If x = 3.8, then
= 3. (2) If x = 3.8, then 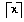 = 4.
= 4.
Definition. The floor function, written floor(x)
or  , is
defined as the largest integer less than or equal
to x.
, is
defined as the largest integer less than or equal
to x.
Examples. (1) If x = 3.0, then  = 3. (2) If x = 3.8, then
= 3. (2) If x = 3.8, then  = 3.
= 3.
Hint: You should be able to reproduce graphs of the ceiling
and floor functions, and various compositions of those functions,
on an exam.
Class #06: Monday 18 Jan 1999
1.3.3.4. Sequences and Summation. We
have thus far examined notation and concepts that support sets, and
operations over sets such as functions. In this class, we will
examine the discrete structure called a sequence, and will
define or analyze various operations over sequences. This will lead
us into the topic of algorithms and complexity in Section 1.4 of these
notes (Chapter 2 of the text), as well as prepare us for a discussion
of number theory (Section 1.5 of these notes and Chapter 2 of the
text).
Concept. A sequence is a discrete structure that
represents an ordered list.
Background. Lists form the basis for data structure
implementations in many digital computing paradigms.
Representation. A sequence is denoted by {an},
which means a list of items denoted by:
{an} = {a1, a2,
..., an} or
{an} = {a0, a1,
..., an-1} .
The two forms are equivalent, but one may be more convenient
in a given application.
Example 1. Let {bn} denote a sequence
comprised of elements bi = (-1)i, i = 0..n-1 .
Then, {bn} = {1, -1, 1, -1, ... }.
Example 2. Let {cn} denote a sequence
comprised of elements ci = 5i, i = 0..n-1 .
Then, {bn} = {1, 5, 25, 125, ... }.
Definition. Given a sequence {an} =
{a1, a2, ..., an},
the summation of {an} is given by
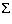 {an}
= a1 + a2 + ... + an =
{an}
= a1 + a2 + ... + an =
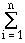 ai .
ai .
Example. Let {an} = {1,3,5,7}. Then,
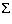 {an} =
1 + 3 + 5 + 7 = 16.
{an} =
1 + 3 + 5 + 7 = 16.
Definition. A sequence {an} is said
to be strictly increasing if ai+1
> ai, i = 1..n-1 .
Example. S = {1,3,5,7} is a strictly
increasing sequence.
Definition. A sequence {an} is said
to be strictly decreasing if ai+1
< ai, i = 1..n-1 .
Example. S = {6, 4, 2, 0, -3, -7} is a strictly
decreasing sequence.
Definition. A sequence {an} is said
to be a geometric progression if it has the form
{an} = {a, a · r, a ·
r 2, a · r 3, ...} .
Example. S = {2, 10, 50, 250,...} is a geometric
progression, where a = 2 and r = 5.
Observation. Summation of a geometric progression
{an} yields a geometric series, of form
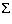 {an}
= a + a · r + a · r 2
+ a · r 3 + ... + a · r n-1 .
{an}
= a + a · r + a · r 2
+ a · r 3 + ... + a · r n-1 .
By substituting the definition of an element in the geometric
progression, the preceding sum can be expressed concisely as
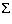 {an} =
{an} =
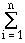 a ·
r i-1 .
a ·
r i-1 .
Derivation. The closed-form analytical expression of
the summation of a geometric sequence {an} with
terms having index zero to n is derived as follows:
Observation. Multiple summation is used in image and signal
processing, as well as in matrix operations. For example,
dual summation of a function f(i,j), where i varies
from 1 to n and j varies from 1 to m, is expressed as:
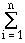
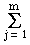 f(i,j)
=
f(i,j)
= 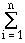 (f(i,1) + f(i,2) + ... + f(i,m))
(f(i,1) + f(i,2) + ... + f(i,m))
 =
f(1,1) + f(1,2) + ... + f(1,m)
=
f(1,1) + f(1,2) + ... + f(1,m)
 +
f(2,1) + f(2,2) + ... + f(2,m)
+
f(2,1) + f(2,2) + ... + f(2,m)
 + ...
+ ...
 +
f(n,1) + f(n,2) + ... + f(n,m) .
+
f(n,1) + f(n,2) + ... + f(n,m) .
Example. Let a sequence S = {f(i,j): f(i,j)
= i + 2j, i,j = 1..3} . Then,
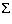 S =
f(1,1) + f(1,2) + f(1,3)
S =
f(1,1) + f(1,2) + f(1,3)
 +
f(2,1) + f(2,2) + f(2,3)
+
f(2,1) + f(2,2) + f(2,3)
 +
f(3,1) + f(3,2) + f(3,3)
+
f(3,1) + f(3,2) + f(3,3)
 = (3 + 5 + 7) + (4 + 6 + 8) + (5 + 7 + 9) = 54 .
= (3 + 5 + 7) + (4 + 6 + 8) + (5 + 7 + 9) = 54 .
One can observe, from the preceding example, that it is
possible for the sum of a sequence generated by a function
to grow as the number of terms in the sequence grows.
This effect is called the growth of functions, which
is basic to the analysis of algorithmic complexity.
1.3.3.5. Growth of Functions. In this section, we discuss
some concepts of complexity, including Big-Oh notation. To
prepare for our exposition of algorithmic complexity in the next
class, you should read Sections 1.7 and 1.8 in the text (Rosen,
Discrete Mathematics and its Applications, 4th Edition).
Concept. It is useful to be able to specify the
complexity of a function or algorithm, i.e., how its
computational cost varies with input size.
Background and Application. Complexity analysis is key to
the design of efficient algorithms. Note that the work or
storage (memory) requirement of a given algorithm can vary
with the architecture (processor) that the algorithm runs on,
as well as the type of software that is being used (e.g.,
runtime modules generated from a FORTRAN versus C++
compiler). Thus, complexity analysis tends to be an approximate
science, and will be so presented in this sub-section.
In particular, when we analyze the complexity of an algorithm,
we are interested in establishing bounds on work,
space, or time needed to execute the computation specified by
the algorithm. Hence, we will begin our exposition of
complexity analysis by analyzing the upper bound on the
growth of a function.
Representation. "Big-Oh Notation" (e.g., O(x2)
reads Big-Oh of x-squared) is used to specify the upper
bound on the complexity of a function f. The bound is
specified in terms of another function g and two
constraints, C and k.
Definition. Let f,g : R -> R be
functions. We say that f(x) = O(g(x))
if there exist constants C,k  R such that
R such that
| f(x) |
 C · | g(x) | ,
C · | g(x) | ,
whenever x > k.
Example. Let f = x3 + 3x2.
If C = 2, then
| f(x) | = | x3 + 3x2 |
 2 · | x3 | ,
2 · | x3 | ,
whenever x > 2. The constants C,k = 2 fulfill the preceding
definition, and f(x) = O(g(x)).
In the next class, we will discuss composition of big-Oh estimates, to
determine an upper bound on the complexity of composite functions and
algorithms.
Class #07: Wednesday 20 Jan 1999
1.4. Algorithms and Algorithmic Complexity
We begin by noting that this is not a class in Algorithms (such
material is covered in COP3530, Algorithms and Data
Structures). Instead, in this class, we use algorithms to
introduce salient concepts and to concentrate on analysis of algorithm
performance, especially computational complexity.
Definition. An algorithm is a finite set of instruction
for performing a computation or solving a problem.
Types of Algorithms Considered. In this course, we will
concentrate on several different types of relatively simple
algorithms, namely:
- Selection -- Finding a value in a list, counting numbers;
- Sorting -- Arranging numbers in order of increasing or
decreasing value; and
- Comparison -- Matching a test pattern with patterns in
a database .
Properties of Algorithms. It is useful for an algorithm
to have the following properties:
- Input -- Values that are accepted by the algorithm are
called input or arguments.
- Output -- The result produced by the algorithm is the
solution to the problem that the algorithm
is designed to address.
- Definiteness -- The steps in a given algorithm must be
well defined.
- Correctness -- The algorithm must perform the task it
is designed to perform, for all input combinations.
- Finiteness -- Output is produced by the algorithm after
a finite number of computational steps.
- Effectiveness -- Each step of the algorithm must be
performed exactly, in finite time.
- Generality -- The procedure inherent in a specific
algorithm should be applicable to all
algorithms of the same general form, with
minor modifications permitted.
Concept. In order to facilitate the design of efficient
algorithms, it is necessary to estimate the bounds on
complexity of candidate algorithms.
Representation. Complexity is typically represented via
the following measures, which are numbered in the order that
they are typically computed by a system designer:
- Work W(n) -- How many operations of each given type
are required for an algorithm to produce specified
output given n inputs?
- Space S(n) -- How much storage (memory or disk) is
required for an algorithm to produce specified
output given n inputs?
- Time T(n) -- How long does it take to compute the
algorithm (with n inputs) on a given architecture?
- Cost C(n) = T(n) · S(n) -- Sometimes called the
space-time bandwidth product, this measure
tells a system designer what expenditure of
aggregate computational resources is required to
compute a given algorithm with n inputs.
Procedure. Analysis of algorithmic complexity generally
proceeds as follows:
Step 1. Decompose the algorithm into steps and operations.
Step 2. For each step or operation, determine the desired
complexity measures, typically using Big-Oh
notation, or other types of complexity bounds
discussed below.
Step 3. Compose the component measures obtained in Step 2
via theorems presented below, to obtain the complexity
estimate(s) for the entire algorithm.
Example. Consider the following procedure for finding
the maximum of a sequence of numbers. An assessment of
the work requirement is given to the right of each statement.
Let {an} = (a1,a2,...,an)
{ max = a1 # One I/O operation
for i = 2 to n do: # Loop iterates n-1 times
{ if ai  max then # One comparison per iteration
max := ai } # Maybe one I/O operation
}
max then # One comparison per iteration
max := ai } # Maybe one I/O operation
}
Analysis. (1) In the preceding algorithm, we note that there
are n-1 comparisons within the loop. (2) In a randomly
ordered sequence, half the values will be less than the
mean, and a1 would be assumed to have the mean
value (for purposes of analysis). Hence, there will be an
average of n/2 I/O operations to replace the value
max with ai. Thus, there are n/2 +
1 I/O operations. (3)This means that the preceding algorithm
is O(n) in comparisons and I/O operations. More
precisely, we assert that, in the average case:
W(n) = n-1 comparisons + (n/2 - 1) I/O operations.
Exercise. In the worst case, there would be n I/O
operations. Why is this so? Hint: This may be a
quiz or exam question.
Useful Terms. When we discuss algorithms, we often use
the following terms:
- Tractable -- An algorithm belongs to class P, such that
the algorithm is solvable in polynomial time
(hence the use of P for polynomial).
This means that complexity of the algorithm is
O(nd), where d may be large
(which typically implies slow execution).
- Intractable -- The algorithm in question requires greater
than polynomial work, time, space, or cost.
Approximate solutions to such algorithms are
often more efficient than exact solutions, and
are preferred in such cases.
- Solvable -- An algorithm exists that generates a solution
to the problem addressed by the algorithm, but
the algorithm is not necessarily tractable.
- Unsolvable -- No algorithm exists for solving the given
problem. Example: Turing showed that
it is impossible to decide whether or not a
program will terminate on a given input.
- Class NP -- If a problem is in Class NP (non-polynomial),
then no algorithm with polynomial worst-case
complexity can solve this problem.
- Class NP-Complete -- If any problem is in Class NP-Complete,
then any polynomial-time algorithm that could
be used to solve this problem could solve all
NP-complete problems. Also, it is generally
accepted, but not proven, that no NP-complete
problem can be solved in polynomial time.
1.4.1. Big-Oh Notation and Associated Identities.
In Section 1.3.3.5, Big-Oh notation was defined. In this section, we
present identities for Big-Oh notation that allow the computation of
complexity estimates for composite functions, with examples.
Theorem 1. (Polynomial Dominance) If
f(x) =  anxn , then f(x) =
O(xn).
anxn , then f(x) =
O(xn).
Example. Find the Big-Oh complexity estimate for n!
Observe that n! = 1 · 2 · 3 · ... · n
 n · n · n · ... · n (n times)
= nn.
n · n · n · ... · n (n times)
= nn.
Hence, n! = O(nn) .
Theorem 2. (Additive Combination) If
f1(x) = O(g1(x))
and f2(x) = O(g2(x)),
then
(f1 +
f2)(x) =
O(max(g1(x),
g2(x)) .
Theorem 3. (Multiplicative Combination) If
f1(x) = O(g1(x))
and f2(x) = O(g2(x)),
then
(f1 ·
f2)(x) =
O(g1(x) ·
g2(x)) .
Example. Estimate the complexity of f(n) =
3n · log(n!).
Step 1. From the previous example, log(n!) is
O(n · log(n)) .
Step 2. Let f1 = 3n and
f2 = log(n!), with f =
f1 · f2 .
Step 3. Note that 3n = O(n).
Step 4. From the law of multiplicative combination
of complexity estimates (Theorem 3, above),
g1(x) · g2(x) =
O(n) · O(n · n log(n)) =
O(n2 · log(n)) .
1.4.2. Big-Omega and Big-Theta Notation.
Big-Oh notation establishes an upper bound on an algorithm's
complexity, since | f(x) |  C · | g(x) | , for x greater than some constant k, given
constant C. (The less-than-or-equal sign denotes that Big-Oh describes
an upper bound).
C · | g(x) | , for x greater than some constant k, given
constant C. (The less-than-or-equal sign denotes that Big-Oh describes
an upper bound).
Concept. To establish a lower bound on
complexity, we use  (called Big-Omega) and
(called Big-Omega) and  (called Big-Theta) notation.
(called Big-Theta) notation.
Definition. If f,g : R -> R
are functions and  C,k
C,k  R+
such that
R+
such that
| f(x) |  C · | g(x) | ,
C · | g(x) | ,
then f(x) is said to be  (g(x)) for all x > k.
(g(x)) for all x > k.
Example. If f(x) = 8x3 + 5x2 +
7, then f(x) is
 (x3), since
f(x)
(x3), since
f(x)  8x3
8x3
 x
x
 R+ .
R+ .
Definition. If f,g : R -> R
are functions, where (a) f(x) is O(g(x))
and (b) f(x) is  (g(x)), then f(x) is
said to be
(g(x)), then f(x) is
said to be  (g(x)),
or Big-Theta of g(x) .
(g(x)),
or Big-Theta of g(x) .
Note: When Big-Theta notation is used, then g(x)
is usually a simple function (e.g., n, nm, log n).
Example. Let f(n) = 1 + 2 + 3 + ... + n. We know
(from previous development) that f(n) =
O(n2). To find a lower bound, note that:

1.5. Integers, Matrices, and Number Theory
Copyright © 1998,1999 by Mark S. Schmalz
All rights reserved, except for viewing/printing by UF faculty
or students registered for this class.
 B
let z = P(x,y), where P(x,y) denotes a
proposition.
B
let z = P(x,y), where P(x,y) denotes a
proposition.
 B.
B.
 q <->
p(x1,x2,...,xn)
= q(x1,x2,...,xn) ,
q <->
p(x1,x2,...,xn)
= q(x1,x2,...,xn) ,
 x1, x2, ...,
xn
x1, x2, ...,
xn  y). This technique allows us to treat the
evaluated relation as a Boolean variable, from which one or
more propositions can be constructed.
y). This technique allows us to treat the
evaluated relation as a Boolean variable, from which one or
more propositions can be constructed.
 y).
y).
 , where
, where 
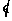 S.
S.
 B
<-> A = {x : x
B
<-> A = {x : x 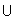 B
= {x : x
B
= {x : x 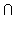 B
= {x : x
B
= {x : x 

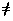 range(g). This is illustrated in the
diagram of Figure 1.4, which illustrates functional
composition graphically.
range(g). This is illustrated in the
diagram of Figure 1.4, which illustrates functional
composition graphically.


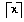 , is
defined as the smallest integer greater than or equal
to x.
, is
defined as the smallest integer greater than or equal
to x.
 , is
defined as the largest integer less than or equal
to x.
, is
defined as the largest integer less than or equal
to x.
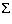 {an}
= a1 + a2 + ... + an =
{an}
= a1 + a2 + ... + an =
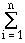 ai .
ai .
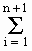 a · r
i-1 =
a · r
i-1 = 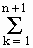 a ·
r k .
a ·
r k .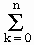 a
· r k + (a · r n+1 - a)
=
a
· r k + (a · r n+1 - a)
= 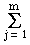 f(i,j)
=
f(i,j)
=  =
f(1,1) + f(1,2) + ... + f(1,m)
=
f(1,1) + f(1,2) + ... + f(1,m)  +
f(2,1) + f(2,2) + f(2,3)
+
f(2,1) + f(2,2) + f(2,3)  anxn , then f(x) =
O(xn).
anxn , then f(x) =
O(xn).
 (called Big-Omega) and
(called Big-Omega) and  (called Big-Theta) notation.
(called Big-Theta) notation.