Class Notes: Data Structures and Algorithms
Summer-C Semester 1999 - M WRF 2nd Period CSE/E119, Section 7344
Homework #1 -- Solutions (in blue type)
Note: There have been many questions about this
homework assignment. Thus, clarifications are posted below
in red type. When you answer these
questions, bear in mind that each one only counts four points
out of 1000 total points for the course. Thus, each one should
have a concise answer. No need to write a dissertation.
- Question 1. Suppose you want to find the maximum of a
sequence or vector a of n distinct
integers. Write an algorithm to do this in O(n)
time, for any sequence of n distinct
integers.
max = very large negative number
input(a)
for i = 1 to n do
if a[i] > max
then max = a[i]
endfor
output(max)
Question 2. You could assume that you
know the maximum value of a before you search for
it. That is, if a has values in the interval [0,101],
then the maximum would be 101. The best case (least
work) in the preceding algorithm would occur when the maximum
of the n-element sequence is the first element of the
sequence. Where is the maximum located for the (a) worst
case, and (b) average case? Support each answer with a
proof, not just an example.
Alternatively, you could assume that the maximum
was not known beforehand, and a)-b), above might be
easier...Either assumption is o.k.
- Case 1: Maximum unknown a priori -- You have to
search through the entire array to find the
maximum. Thus, there is no worst case or best
case if you consider the work as comparisons
(dominant cost) only.
- Case 2: Maximum known a priori -- This becomes a linear
search problem (find the maximum). Thus, the
best case is when the maximum is in the first
position (a[1], only one comparison required to
find the maximum value), and the worst case when
it is at the n-th position (a[n], n-1
comparisons required).
- Case 3: Ascending/descending sequence -- This is the
easiest case. In an ascending (descending)
sequence, the maximum is at the end (beginning)
of the sequence, i.e., a[n] (a[1]). Thus, there
is no best or worst case, since you know where
the maximum is, and only O(1) I/O ops are
required.
Question 3. Given the algorithm you developed in
Question 1 including whatever assumptions on
which you based your development and analysis for the
best, worst, and average cases, what is the computational work
requirement W for finding the maximum
in the (a) best, (b) worst, and (c) average case? Show
your work for each case - it is best to compute W for each step of the algorithm, then sum
W over all steps to get the total work
requirement Wtot .
- Answer: The complexity budget depends on how you
wrote the algorithm. Given the algorithm shown above,
we have the following complexity budget:
EXT.I/O MEM.I/O COMPARISONS INCR
max = very large negative number 1
input(a) n
for i = 1 to n do n-1
if a[i] > max 1 1 to n
then max = a[i] 1 to n
endfor
output(max) 1
Total cost is thus (n+1) external I/O ops, between 3 and (n+3)
memory I/O ops, between 1 and n comparisons, and n-1
incrementations of the loop index. Worst case is n comparisons,
best case is 1 comparison, so we say the average case is (n+1)/2
comparisons, which is approximated by n/2.
Question 4. If you have a sequence of n distinct
integers, what is the probability that (a) the maximum of the sequence will occur as the first
element of the sequence, or (b) as the last element of the
sequence? Show your work, and give an example, using a
5-element sequence.
- Case 1: Maximum unknown a priori -- Probability of
occurrence of any value in any position is 1/n.
This obviously applies to the maximum.
- Case 2: Maximum known a priori -- Probability of
occurrence in first position is 1/n.
Probability of occurrence in last position is
(n-1)! / (n!) = 1/n, if ordering is important.
- Case 3: Ascending/descending sequence -- In an
ascending (descending) sequence, the maximum is
at the end (beginning) of the sequence. Hence
the probability of the maximum being at the
beginning (end) of an ascending sequence is 0
(1), and symmetrically for a descending sequence.
Question 5. Given a sequence of n distinct integers,
what is the probability that the maximum of the sequence will
occur as the i-th element of the sequence, where i = 1..n?
For Question 6, denote this probability as
Pr(max @ i).
Show your work, and express the probability as a function
of the index i.
- Case 1: Maximum unknown a priori -- Probability of
occurrence of any value in any position is 1/n.
- Case 2: Maximum known a priori -- Probability of
occurrence in i-th position is P(n,i)/n!,
where P(n,i) denotes the number of
i-permutations of n things.
- Case 3: Ascending/descending sequence -- See Case 3 of
the solution to Question 4. The probability of
the maximum being at the end (beginning) of an
ascending (descending) sequence is 1, and is
zero elsewhere.
Question 6. Taking the result you obtained in Question
5, derive a technique for determining the average
probability of occurrence of the
maximum of an n-element sequence. Hint: Sum the
probability Pr(max @ i) over i = 1..n, then
divide the sum by n.
- Case 1: Maximum unknown a priori -- Probability of
occurrence of any value in any position is 1/n,
so the average probability is 1/n.
- Case 2: Maximum known a priori -- Probability of
occurrence in i-th position is P(n,i)/n!,
where P(n,i) denotes the number of
i-permutations of n things.
Expression:
Prave =
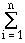 P(n,i)/n! .
P(n,i)/n! .
Case 3: Ascending/descending sequence -- The probability
of the maximum occurring at either the end or
the beginning of the sequence is 1, and zero
for the other n-1 positions. So, the average
probability is 1/n = (1+0+0+...+0)/n =
(0+0+...+0+1)/n or
To get credit for Question 6, you must (a) show an example worked
out by hand, in detail, for a 5-element sequence; and (b)
compare this probability with the probability of the average
work requirement Wave. Hint: You were asked to
deduce Wave in Question 3.
If you chose either Case 1 or Case 3, you would
have the average probability as 1/n, regardless of the position
of the maximum. In Case 1, the average work is n comparisons,
the same as the best or worst case, so the probability of average
work is 1, versus 1/n for the position. In Case 2, you would have
to compute the probability, per the answer shown above. In Case
3, the probability of finding the maximum on the first try is
1.0, and that represents the average case. The probability of
finding the maximum if you choose position randomly is 1/n.
Note: Ask the TAs if you have questions about the homework.
You must complete the homework by yourself, but you can work
together on general approaches to solving the homework problems.
Show your work to get full credit. Any copying will be construed
as cheating.
Copyright © 1999 by Mark S. Schmalz.
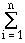 P(n,i)/n! .
P(n,i)/n! .