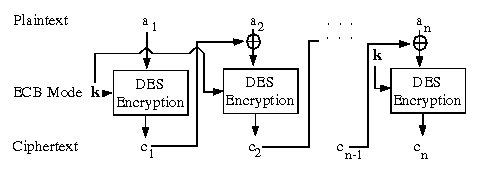
Figure 3.3.1. DES cipher-block chaining mode.
Disadvantages. The sender(s) and receiver(s) share a secret key. This leads to quadratic complexity of key distribution over a network, which we discussed in Section 3.2.
We begin our discussion of public-key cryptography (PKC) applications by reviewing several topics that were mentioned in the introduction to Section 3.2. We then progress to a discussion of authentication, digital signatures, and message digests (Section 3.3.2).
The topic of message integrity leads naturally into a discussion of digital signatures (DSs, Section 3.3.2). It is desirable that DSs have the following attributes:
Additionally, it is useful for hash functions (where the hash size is smaller than the message) to have collision freedom, which can be specified as follows:
'
such that y = h(x').
This property is especially
desirable in systems where a hash is sent instead of sending the
actual message.
'
such that h(x) =
h(x') .
We next progress to the description of digital signatures and message digests.
Note: We especially want to obviate cut-and-paste attacks, which can be done with chaining or reduction. With chaining, messages that the sender signs are joined and sent as one message. Reduction hashes a long message into blocks that the sender signs. This achieves integrity and authentication of the sender.
One approach to achieve integrity via chaining is to use DES with a Cipher Block Chaining (CBC) residue. Recall (from Section 3.1) that there are three modes of DES usage, namely, Electronic Code Book (ECB), Cipher Feedback Mode (CFM, which facilitates stream ciphers), and CBC.

Figure 3.3.1. DES cipher-block chaining mode.
Disadvantages. The sender(s) and receiver(s) share a secret key. This leads to quadratic complexity of key distribution over a network, which we discussed in Section 3.2.
Thus, it is preferable to employ an PKC/RSA based solution. An instance of this method is called Public Signatures, which we discuss as follows.
Algorithm. If the preceding assumption holds, then
Advantages. Since only Alice can read e(a,kA), we have secrecy. Since only Alice can produce e(a,kA-1), some degree of authenticity can be implemented.
Disadvantages. Unfortunately, if one encrypts with a public key, one does not have verifiability via examination of the encryption by a third party.
Observation. For two-party RSA (e.g., Alice and Bob), we have keys (kA,kA-1) and (kB,kB-1). The order of encryption is important. That is, if Bob is sending a message a to Alice, should we encrypt with kB then kA-1, or vice versa? The latter method is preferred (i.e., {{a}kA-1}kB), since
 K,
K,
 S such that
sigk : P -> A, and
S such that
sigk : P -> A, and  V such that
verk : P × A -> {0,1},
V such that
verk : P × A -> {0,1},  where
verk is given by
where
verk is given by
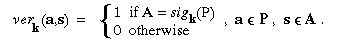
Remark. Signature schemes have the following desirable properties, which are symmetric to those enumerated at the end of Section 3.3.1. Namely, it should be hard to
'
for any given x, such that
sigk(x') =
sigk(x). This helps avoid forgery.
' such that
sigk(x') =
sigk(x).
We next overview Lamport's One-time Signature Scheme (LSS), a variation of the preceding signature scheme.
Algorithm. Given the foregoing assumption, Lamport's signature scheme involves the following steps:
 {0,1}
and keep them secret.
{0,1}
and keep them secret.
Step 2. Compute 2n elements yi,j =
f(xi,j), for i = 1..n, and j
 {0,1}.
{0,1}.
Step 3. Let a message a
 P
be partitioned bitwise as (a1, a2, ...,
an). The sig function is given by
P
be partitioned bitwise as (a1, a2, ...,
an). The sig function is given by
sigk(a1, a2, ..., an) = (x1,a1, x2,a2, ..., xn,an) .
Step 4. Given a signature s A = P
partitioned bitwise as (s1, s2, ...,
sn), the ver function is given by
A = P
partitioned bitwise as (s1, s2, ...,
sn), the ver function is given by
verk(a1, a2, ..., an, s1, s2, ..., sn) = 1 ,
if and only if for all i {1,2,...,n},
f(si) = yi,ai .
{1,2,...,n},
f(si) = yi,ai .
Observation. The spaces X and Y must be large, such that guessing the function f incurs a prohibitively large search cost.
 FN,
FN,
Step 2. A DES-like encryption scheme is applied to text input and kDES, where the expansion permutation is modified by a 12-bit mask. The modified expansion permutation converts 32 bits into 48 bits. Additionally, the mask is randomly reset whenever the user's password is changed.
Step 3. The DES output is an encrypted password that is assigned to storage as the user's password.
 Zp* exists if and only if
all y
Zp* exists if and only if
all y  Zp* are nontrivial powers of x.
Zp* are nontrivial powers of x.
Assumption. Let p be a prime number such that log(p)
 Zp is hard to compute. Additionally, let
Zp is hard to compute. Additionally, let

 Zp* be a primitive element. Using the
cryptosystem formalism developed in the preceding section, let
plaintext P = Zp* and let
authentication codes
Zp* be a primitive element. Using the
cryptosystem formalism developed in the preceding section, let
plaintext P = Zp* and let
authentication codes
A = Zp*
× Zp-1.
Observation. Given the preceding assumption, let the keyspace
K = {( ,
,
 , a,
, a,
 ) :
) :
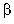 =
=
 a mod p }.
a mod p }.
Definition. Let k  (Zp-1)*
and let
(Zp-1)*
and let  =
=
 k mod p.
Denote the plaintext
x
k mod p.
Denote the plaintext
x P
and let
P
and let
 = (x -
= (x -

 ) · k-1 mod (p - 1).
) · k-1 mod (p - 1).
Definition. Given the preceding definition, let
sigk(x,k) =
( ,
,
 )
)
 verk(x,
verk(x,
 ,
,
 ) = 1
<=>
) = 1
<=>
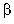
 ·
· 
 ~
~  x mod p.
x mod p.
 (I)
(I)
 a
a ·
·  k
k = (
= ( a)
a) (
( k)
k) ~
~
 x mod p
x mod p
 =
=  a
a ·
·  k(x -
k(x - 
 ) · k-1 mod (p-1) ~
) · k-1 mod (p-1) ~
 x mod p
x mod p
 =
=  a
a + x-
+ x-
 =
=  x .
x .
Observation. Possible attacks on the El Gamal cryptosystem include:
 -1
· (x -
-1
· (x -  k)
=
k)
=  , which is hard
because an adversary must simultaneously choose correct values
for a, k, and
, which is hard
because an adversary must simultaneously choose correct values
for a, k, and  .
.
 ,
,
 , and x
simultaneously. For example, let
, and x
simultaneously. For example, let  Z such that
0
Z such that
0 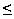 i,j
i,j
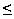 p-2 and
gcd(j, p-1) = 1. Additionally let:
p-2 and
gcd(j, p-1) = 1. Additionally let:
 =
=
 i
i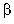 j mod p
j mod p  =
-
=
- j-1
mod p-1
j-1
mod p-1  i j-1
mod p-1,
i j-1
mod p-1, where j-1 is taken modulo p-1. Now, observe that
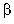


 ~
~ 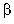
 (
( i
i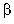 j)
j)

 ~
~ 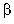
 (
( i
i
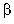 j
j )
)
 ~
~ 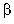

 i(-
i(- j-1) mod p-1
j-1) mod p-1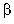 j(-
j(- j-1) mod p-1
j-1) mod p-1
 ~
~ 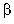

 -
- i j-1
i j-1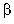 -
- ~
~  -
- i j-1
~
i j-1
~  x .
x .
 ,
,
 , i, j, etc.
This is a weakness of the El Gamal cryptosystem,
but not an implementationally significant one.
, i, j, etc.
This is a weakness of the El Gamal cryptosystem,
but not an implementationally significant one.
Observation. If the unique, randomly-chosen k =
(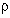 ,
,
 ,
,
 ,
,
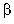 )
is compromised, it is possible that knowledge of k
will reveal the secret value a.
If k is revealed for (x,
)
is compromised, it is possible that knowledge of k
will reveal the secret value a.
If k is revealed for (x,
 ,
,
 ),
then
),
then
a = (x - k )
)
 -1
mod (p-1)
-1
mod (p-1)
 = (x - a
= (x - a )
k-1 mod (p-1) .
)
k-1 mod (p-1) .
 =
x - a
=
x - a ,
,
a = (x - k )
)
 -1
mod (p-1) .
-1
mod (p-1) .
Remark. Implementationally, every reuse of k reinforces an adversary's trial of previous attacks. When Oscar finds two messages that yield to the same attack, he can compute k and then obtain the desired signature.
The Digital Signature System (DSS) is another method of digitally signing messages that features small signatures and a large modulus (to make the discrete key hard to guess). DSS has reduction in the exponent that allows (for example) a 160-bit message, which implies a 320-bit signature by a 512-bit modulus.
The following changes to the El Gamal cryptosystem are encountered in DSS:
 = (x + a
= (x + a )
k-1 mod (p-1).
)
k-1 mod (p-1).  x
x
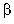
 =
= 
 mod p .
mod p .
Note: If gcd(x +
a , p-1) = 1, then
, p-1) = 1, then
 -1 mod p-1
exists and the preceding equation becomes
-1 mod p-1
exists and the preceding equation becomes
 x
x -1
-1
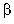

 -1
=
-1
=  mod p .
mod p .
A key implementational issue is the probability of successful attack. We begin by discussing the Birthday Attack, which provides information about a lower bound on digest size.
Q = N(N-1)/2M ,
and hence is of order N2.Example. For a birthday attack where M = 365, we have that
Q = N(N-1)/730
 and
and
 730
730 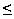 N(N-1)
< N2 .
N(N-1)
< N2 .
Remark. Finding one-way functions that perform the appropriate reduction is a difficult goal, since there are many unresolved questions associated with hash functions. For example, the use of trapdoors, trick constants, etc. that permit Government agencies to access encrypted data.
An early message digest implementation called MD2 employed (a) 8-bit arithmetic; (b) few intermediate values, thereby yielding low space complexity; and (c) one-pass computation.
Step 2. Pad the concatenation of the partitions obtained in Step 1 to the nearest multiple of 16 bytes.
Step 3. Add a 16-byte checksum.
Step 4. Perform digest computation on 16-byte blocks.

 -substitution,
which is customarily based on digits of
-substitution,
which is customarily based on digits of
 taken in 8-bit
partitions, where repeated results are discarded. The
taken in 8-bit
partitions, where repeated results are discarded. The
 -substitution is
employed as shown in the following schematic diagram:
-substitution is
employed as shown in the following schematic diagram:
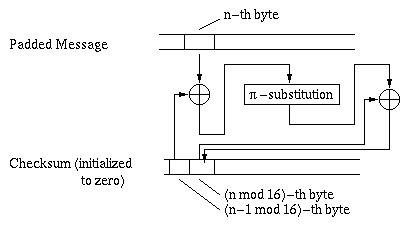
checksum(a[n mod 16]) =



checksum(a[n mod 16])
XOR
 (checksum(a[n-1 mod 16],
msk[n]) ,
(checksum(a[n-1 mod 16],
msk[n]) ,
Step 4 - Digest Computation: The message digest is computed via the following architecture:
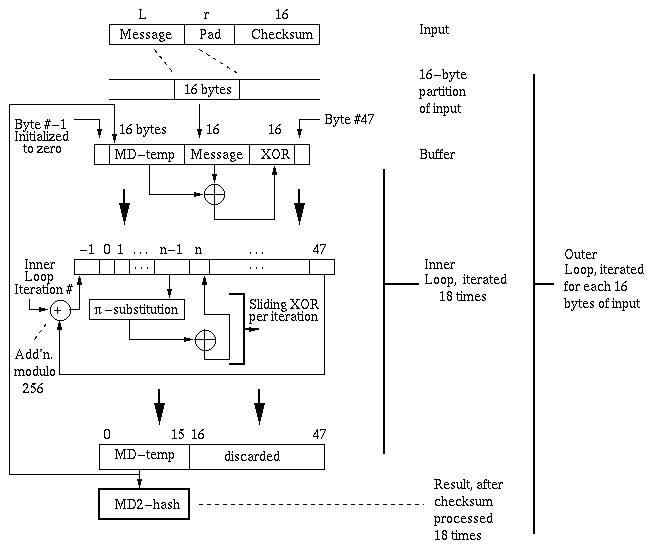
As time progressed, the development of integrated-circuit CPUs soon rendered MD2's byte-oriented algorithm obsolete. Thus, MD4 was introduced, which implemented the following advances:
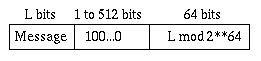
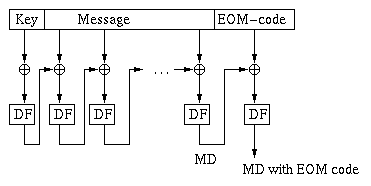
For example, secret sharing between two parties (Alice and Bob) employs the following procedure:
MIC = MD(KAB · a) ,
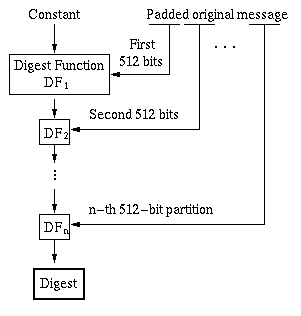
where the digest function DF is applied recursively as follows:
In practice, one partitions a message as a = (a1, a2, ..., an) and employs keys k1, k2, ..., kn. The encryption function e is then applied as:
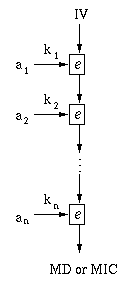
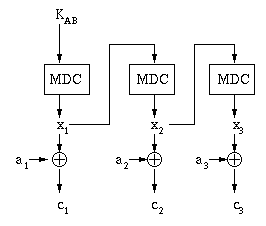
Disadvantages: This system is vulnerable for at least two reasons:
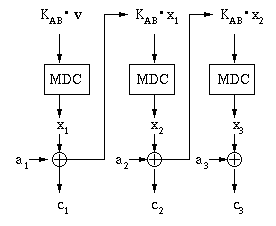
Disadvantage: Cut-and-paste attacks are possible, but can be avoided by concatenating K with ciphertext partition ci instead of xi.
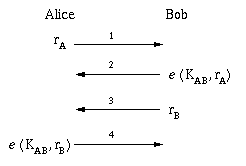
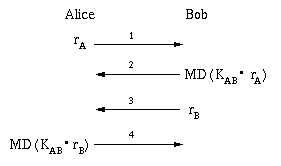
This concludes our overview of public-key cryptosystem applications. We next dicuss implementational aspects of PKC.