Cryptology - I: Symbols and Notation
In this class, we must express cryptologic transformations and
operations in a rigorous fashion, in order to (a) understand their
structure and function, (b) predict consequences of changing transform
parameters, and (c) have a unified basis for comparing cryptographic
algorithms. Currently, the only rigorous, concise notation that unifies
image and signal processing (of which cryptology is a part) is called
image algebra. Some of you may have heard of this notation, which
was invented here at UF by Gerhard Ritter. Image algebra is a rigorous,
concise notation that unifies linear and nonlinear mathematics
in the image domain. Image algebra was developed at UF under DARPA and Air
Force support since the early 1980s to provide a simple, powerful notation
for describing image and signal processing algorithms in a unified, high-
level manner.
The following theory is a small subset of image algebra, since
the aim of this class is not to teach the details of image
algebra. Rather, we are teaching basic cryptology within the context of
image algebra, for the above-mentioned reasons. Thus, we provide the
following brief theoretical introduction.
NOTE: Bold-italic-face titles or names denote cryptologic
terms that we will use in class.
1. Sets and Set Operations
Sets are the basic entities in image algebra and are the building blocks
of mappings that we will subsequently use to define images. A few concepts
and conventions are noteworthy:
- Sets are customarily denoted by upper-case letters
in roman (regular) or italic face (e.g., A, G), or by the
empty set Ø.
- Value Sets or Alphabets are denoted by bold upper-case
letters from the head of the alphabet (e.g., A, B, ...).
Additionally, we call F the generalized value set.
Commonly-used value sets include the
Furthermore, we have the integers modulo n, which
are denoted by Zn. In the special case of the
binary numbers, we write B
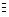 Z2 for purposes
of brevity.
Z2 for purposes
of brevity.
Intervals. Occasionally, we use a concise specification of a
contiguous subset of a given set, called an interval. For
example, [1,4] Z
denotes the set {1,2,3,4}, while the half-open interval
(1,4]
Z
denotes the set {1,2,3,4}, while the half-open interval
(1,4] Z denotes
the set {2,3,4}. Similarly,
(2,4]
Z denotes
the set {2,3,4}. Similarly,
(2,4] R =
{x
R =
{x R:
2 < x
R:
2 < x 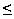 4}.
4}.
- Point Sets, Domain Sets, or Domains are denoted by
bold upper-case letters from the tail of the alphabet (e.g.,
U, V, W, X, and Y). Additionally,
we call X the generalized point set.
Customary point sets include
- Set Operations.
The customary set operations of union
(
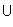 ), intersection
(
), intersection
(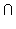 ),
subtraction (\), complement (´), cardinality (|A|),
choice (choice), infimum (inf), and
supremum (sup) are supported.
),
subtraction (\), complement (´), cardinality (|A|),
choice (choice), infimum (inf), and
supremum (sup) are supported.
Unary arithmetic functions are applicable to subsets of the real
numbers (e.g.,
max or 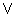 ,
min or
,
min or 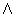 ,
and abs). Note that
abs denotes absolute value of a set instead of |A|,
which is reserved for cardinality.
,
and abs). Note that
abs denotes absolute value of a set instead of |A|,
which is reserved for cardinality.
2. Images or Messages
One usually thinks of an image as a two-dimensional array of reals or
integers. Unfortunately, that definition is too restrictive for modern
image and signal processing, of which cryptography and cryptanalysis are
a part. Thus, we use the image algebra definition of an image, which
generalizes all images.
- If a
 FX, then
X = domain(a) and
F = range(a).
FX, then
X = domain(a) and
F = range(a).
- Although a point set or value set can be any set, one must take
care to specify images using only those value or point sets for
which operations are defined.
3. Image Operations.
In order to manipulate images or messages, we must specify a few simple
operations. Fortunately, cryptology is not as complex notationally as image
processing, so we can concentrate on the pointwise unary and binary
operations that are frequently used in cryptography, as well as simple
image-template operations (Section 6).
- A binary pointwise image operation
g:FX × FX
-> FX is induced over X by the
corresponding scalar operation g:F × F
-> F. Note that the operands (input images) must have the
same domain, which the result (output image) also has.
Example. Given the images a,b
 FX,
we have the pointwise arithmetic operations
FX,
we have the pointwise arithmetic operations
c = a + b 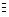 {(x, c(x)) : c(x) =
a(x) + b(x), where
a(x),b(x)
{(x, c(x)) : c(x) =
a(x) + b(x), where
a(x),b(x)
 R,
x
R,
x  X}
X}
c = a · b
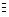 {(x, c(x)) : c(x) =
a(x) · b(x), where
a(x),b(x)
{(x, c(x)) : c(x) =
a(x) · b(x), where
a(x),b(x)
 R,
x
R,
x  X} .
X} .
Example. If a and b are Boolean images on
X, then we have the following definition of the
exclusive-or function:
c = (a xor b)
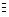 {(x, c(x)) : c(x) =
|a(x) - b(x)|,
x
{(x, c(x)) : c(x) =
|a(x) - b(x)|,
x  X} .
X} .
Observation. A wide variety of binary operations can be
described (e.g., ab and logab),
provided that value sets are properly defined. However, in the
case of the logarithm, we must set
range(a), range(b)
 R+, the positive reals. Otherwise, the logarithm
is not defined.
R+, the positive reals. Otherwise, the logarithm
is not defined.
- A special type of binary operation is called the restriction
of an image a
 FX to a subset
W of its domain X, which is denoted by:
FX to a subset
W of its domain X, which is denoted by:
b = a|W
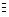 {(x, b(x)) : b(x) =
a(x), x
{(x, b(x)) : b(x) =
a(x), x W
W X} .
X} .
The converse of restriction is extension. For example, the
extension of image b  FW to a k-valued
constant image on X, the domain of a, is denoted by:
FW to a k-valued
constant image on X, the domain of a, is denoted by:
c = b | k
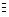 {(x, c(x)) : c(x) =
b(x) if x
{(x, c(x)) : c(x) =
b(x) if x
 W or
c(x) = k(x) if x
W or
c(x) = k(x) if x
 X\W} .
X\W} .
An image can also be restricted to a subset of its range space.
Assuming that a  FX and
A
FX and
A  F,
we have the following notation:
F,
we have the following notation:
b = a ||A
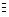 {(x, b(x)) : b(x) =
a(x) if
a(x)
{(x, b(x)) : b(x) =
a(x) if
a(x) A
A F,
x
F,
x X} .
X} .
Implementationally, image restriction can be thought of as a
cut operation, while extension can be thought of as a
paste operation.
- Another binary operation is called the characteristic
function of an image a
 FX. Let S denote a property of a's
range space (for example, "
FX. Let S denote a property of a's
range space (for example, " A
A
 F", such that
F", such that
b =
 S(a)
S(a)
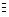 {(x, b(x)) : b(x) =
1 if a(x) satisfies S, or b(x) = 0
otherwise}.
{(x, b(x)) : b(x) =
1 if a(x) satisfies S, or b(x) = 0
otherwise}.
The resultant image b is a Boolean image on X.
Thus, the characteristic function can be thought of as a logical
test with predicate S that returns a Boolean image. Wherever the
test condition S is satisfied, a unitary value occurs, with zeroes
elsewhere.
Example. The characteristic function can be employed in
thresholding an image a  RX using a real threshold T, as follows:
RX using a real threshold T, as follows:
b =
 >T(a)
>T(a)
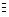 {(x, b(x)) : b(x) =
1 if a(x) > T, or b(x) = 0
otherwise}.
{(x, b(x)) : b(x) =
1 if a(x) > T, or b(x) = 0
otherwise}.
4. Domain Transformations.
An important class of encryptions are called transpostions,
in which the domain of a plaintext message is manipulated so that
the symbol order is rearranged. Let a denote an image in
FX, and define a spatial transformation
f: Y -> X. For purposes of simplicity,
assume that f is a one-to-one and onto mapping.
The composition of a with f is denoted by:
b = a o f
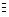 {(y, b(y)) : b(y) =
a(f(y)), y
{(y, b(y)) : b(y) =
a(f(y)), y
 Y} .
Y} .
The combination of pointwise operations and domain transformations
can produce powerful encryptions, as we shall see when we consider
the DES transformation. It is interesting to note that in image
processing, spatial transformations are used for image magnification,
rotation, and warping.
5. Templates.
The most powerful construct in image algebra is called a
template, which is defined as a mapping from a point set
to a set of images. Thus, a template is an image whose pixel
values are images.
- Templates are denoted by bold, lower-case letters from the tail
of the alphabet
(e.g., r, s, ...).
- We say that t
 (FX)Y is an
F-valued template
from Y to FX.
This means that a template value t(y)
(FX)Y is an
F-valued template
from Y to FX.
This means that a template value t(y)
 FX, where
y
FX, where
y Y, is an
image on X. For purposes of notational brevity, we write
ty
Y, is an
image on X. For purposes of notational brevity, we write
ty 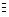 t(y).
Note that ty =
{(x,ty(x)):
x
t(y).
Note that ty =
{(x,ty(x)):
x  X} .
Thus, a value of t's weight
matrix ty, also called a weight of
template t, is expressed as
ty(x)
X} .
Thus, a value of t's weight
matrix ty, also called a weight of
template t, is expressed as
ty(x)  F. Additionally, we denote the support of
ty as S(ty)
F. Additionally, we denote the support of
ty as S(ty)
 X. Implementationally,
we usually think of the support as the set of domain points
corresponding to the template's nonzero weights. Although this
definition is not
X. Implementationally,
we usually think of the support as the set of domain points
corresponding to the template's nonzero weights. Although this
definition is not
general, it will be sufficient for this
class.
Templates generalize the concepts of convolution masks, filter
domains, sampling windows, etc., and thus provide a unifying
construct for describing neighborhood operations on images.
We rarely use templates in cryptography, but employ
them extensively in cryptanalysis, particularly for pattern
matching and correlation-based attack. These strategies
will be discussed at length when we consider substitutional and
transpositional ciphers.
6. Image-Template Operations.
Images and templates are combined using the generalized
image-template left product
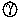 :
FX ×
(FX)Y ->
FY, which accepts an image and a
template and returns an image.
:
FX ×
(FX)Y ->
FY, which accepts an image and a
template and returns an image.
- Given the associative, commutative
operations
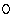 ,
, : F × F -> F, an image
a
: F × F -> F, an image
a  FX, and a template
t
FX, and a template
t  (FX)X, the
left product is defined as
(FX)X, the
left product is defined as
(a 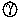 t)y =
t)y =
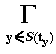 a(x)
a(x) 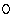 ty(x) , y
ty(x) , y
 Y .
Y .
The right product
t 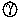 a
is symmetrically defined.
a
is symmetrically defined.
Example. When  = + and
= + and 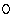 = ·, we have
the linear convolution
= ·, we have
the linear convolution
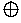 , which is defined
in terms of the left product as
, which is defined
in terms of the left product as
(a 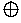 t)y =
t)y =
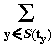 a(x) · ty(x) ,
y
a(x) · ty(x) ,
y  Y .
Y .
If t is a template from X to X and a is
an image on X, then a
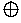 t =
t
t =
t 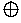 a.
a.
Example. When  =
= 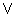 and
and
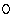 = ·, we have
the multiplicative maximum operation
= ·, we have
the multiplicative maximum operation
 , and when
, and when
 =
= 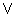 and
and
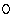 = +, we have
the additive maximum operation
= +, we have
the additive maximum operation
 . The operations of
multiplicative minimum and additive minimum are symmetrically
defined.
. The operations of
multiplicative minimum and additive minimum are symmetrically
defined.
Although we will not use the nonlinear operations
 or
or
 extensively in this class,
such operations can be employed in cryptanalysis, especially
for nonlinear analysis attack on compressed or encrypted signals.
The topic of nonlinear cryptanalysis will be mentioned at the
end of the semester, if time permits.
extensively in this class,
such operations can be employed in cryptanalysis, especially
for nonlinear analysis attack on compressed or encrypted signals.
The topic of nonlinear cryptanalysis will be mentioned at the
end of the semester, if time permits.
This concludes our discussion of basic notation for this class. Other
notational conventions will be defined as they are introduced in
theory development.
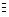 Z2 for purposes
of brevity.
Z2 for purposes
of brevity.  Z
denotes the set {1,2,3,4}, while the half-open interval
(1,4]
Z
denotes the set {1,2,3,4}, while the half-open interval
(1,4] Z denotes
the set {2,3,4}. Similarly,
(2,4]
Z denotes
the set {2,3,4}. Similarly,
(2,4] R =
{x
R =
{x R:
2 < x
R:
2 < x 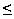 4}.
4}.
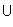 ), intersection
(
), intersection
(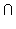 ),
subtraction (\), complement (´), cardinality (|A|),
choice (choice), infimum (inf), and
supremum (sup) are supported.
),
subtraction (\), complement (´), cardinality (|A|),
choice (choice), infimum (inf), and
supremum (sup) are supported. 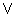 ,
min or
,
min or 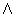 ,
and abs). Note that
abs denotes absolute value of a set instead of |A|,
which is reserved for cardinality.
,
and abs). Note that
abs denotes absolute value of a set instead of |A|,
which is reserved for cardinality.
 a =
a =
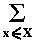 a(x)
a(x)
 S(a)
S(a)
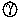 :
FX ×
(FX)Y ->
FY, which accepts an image and a
template and returns an image.
:
FX ×
(FX)Y ->
FY, which accepts an image and a
template and returns an image.
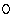 ,
, : F × F -> F, an image
a
: F × F -> F, an image
a 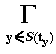 a(x)
a(x) 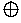 , which is defined
in terms of the left product as
, which is defined
in terms of the left product as
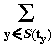 a(x) · ty(x) ,
y
a(x) · ty(x) ,
y  , and when
, and when
 . The operations of
multiplicative minimum and additive minimum are symmetrically
defined.
. The operations of
multiplicative minimum and additive minimum are symmetrically
defined.