Cryptology - I: Homework 1 - Mono- and Poly-alphabetic Ciphers

Instructors: R.E. Newman-Wolfe and M.S. Schmalz

In this homework, we cover shift, substitution, and Vigenere ciphers. All problems are taken from the textbook (Stinson). Many thanks to Jim Wei and Eric Chung for sharing their solution files with us, which we have modified to form this Web page.

Problem 1.1. Below are given four examples of ciphertext, obtained from Substitution, Vigenere, Affine, and unspecified ciphers. Provide the plaintext and explain how you obtained the solution.

1.1 a) Substitution Cipher. The technique here is to compute the sorted histogram of both ciphertext and a similar plaintext corpus. You have the advantage in the latter case of Table 1.1 on page 26 of Stinson. By matching the first two quintiles of characters (to preserve a high signal-to-noise ratio), you can obtain some guesses about letters. Here is the ciphertext and plaintext juxtaposed, followed by the method Jim used to solve the problem:

Ptxt: imaynotbeabletogrowflowersbutmygardenproduces
Ctxt: EMGLOSUDCGDNCUSWYSFHNSFCYKDPUMLWGYICOXYSIPJCK
 
      justasmanydeadleavesoldovershoespiecesofropea
      QPKUGKMGOLICGINCGACKSNISACYKZSCKXECJCKSHYSXCG

      ndbushelsofdeadgrassasanybodysandtodayibought
      OIDPKZCNKSHICGIWYGKKGKGOLDSILKGOIUSIGLEDSPWZU

      awheelbarrowtohelpinclearingitupihavealwayslo
      GFZCCNDGYYSFUSZCNXEOJNCGYEOWEUPXEZGACGNFGLKNS

      vedandrespectedthewheelbarrowitistheonewheele
      ACIGOIYCKXCJUCIUZCFZCCNDGYYSFEUEKUZCSOCFZCCNC

      dvehicleofwhichiamperfectmaster
      IACZEJNCSHFZEJZEGMXCYHCJUMGKUCY

Deciphered Plaintext:

I may not be able to grow flowers but my garden produces just as many dead leavesl, old overshoes, pieces of rope, and bushels of dead grass as anybody's. And today I bought a wheelbarrow to help in clearing it up. I have always loved and respected the wheelbarrow.
It is the one wheeled vehicle of which I am perfect master.

Ctxt: A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z
Freq: 5     37 8  12 9  24 5  15 7  18 7  5  13 10 6  1     20    14    5  7  15 13
Rank: 21    1  13 10 12  2 19  6 14 4  15 20 9  11 17 22    3     7     18 16 5  8
Ptxt: v     e  b  i  w  a  f  d  c  s  y  m  l  n  u  j     o     y     g  p  r  h

Analysis:
C -> e - because C is most frequent  
Q -> j - because both only occur once
Z -> h - There are 7 ZC's, but only 1 CZ, and HE is 2nd most
	   frequent digram.
       - Also there are 4 ZCN's, and HER is 4-th most popular trigram.
N -> l - A guess that worked
U -> t - There are 2 UZC's, and THE is the most frequent trigram
       - Also 1 CU and 2 UC's (with TE and ET corresponding) are on the 
	   digram list, but their frequencies are low.
S -> o - As in l-ved, o and i both fit, o was tried first and it worked.
O -> n - GO occured 5 times, and is a frequent English digram.
K -> s - K is 4th most popular letter and cannot be a vowel, otherwise we
           would frequently have three consecutive vowels (e.g., CKS).
I -> d - ICGI, which decrypts to -ea- becomes "dead"
           Similarly,lea-e- is probably leaves.
A -> v - From the I->d substitution, NCG-C is lea-e => leave
W -> g - WYGKK => -rass, which is "grass".
L -> y - An easy guess: alwa-s => always.
X -> p - Since res-e-ted should be "respected"
J -> c - As in the preceding substitution, respe-ted should be "respected"
E -> i - An easy guess: veh-cle is "vehicle".
P -> u - Another easy one: prod-ces is "produces".
D -> b - "-ought" => "bought" and "wheel-arrow" => "wheelbarrow".
M -> m - "I-aynot" => "I may not"

1.1b) Vigenere Cipher

Ciphertext:

        KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUD
        DKOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYC
        QKYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRL
        SVSKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMV
        GKMITZHFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFS
        PEZQNRWXCVYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHI
        FFSQESVYCLACNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIY
        CWHJVLNHIQIBTKHJVNPIST

Step 1. Apply the Kasiski Test to find that the trigram HJV occurs five times at positions 108, 126, 264, 318, and 330. The intervals are 18, 138, 54, and 12, which are divisible by 2, 3, and 6. So the keyword length is either 2, 3 or 6.

Step 2. Assuming the longest key, we compute the Index of Coincidence(I_c):

        Column  2       3       4       5       6       7       8
        1       0.044   0.064   0.049   0.057   0.079   0.050   0.056
        2       0.0524  0.056   0.054   0.057   0.097   0.062   0.062
        3               0.057   0.049   0.048   0.066   0.063   0.057
        4                       0.060   0.049   0.082   0.061   0.063
        5                               0.057   0.060   0.064   0.062
        6                                       0.090   0.064   0.068
        7                                               0.061   0.063
        8                                                       0.077

This also provided strong evidence that the keyword length is 6, since the higher values occurred in row and column 6.

Step 3. We next compute the 390(15x26) Mutual Index of Coincidence (MI_c), with the resulting relative shifts listed as:

        K1 - K2 = 11
        K1 - K3 = 4
        K1 - K4 = 13
        K1 - K5 = 9
        K1 - K6 = 14
        K2 - K3 = 19
        K2 - K4 = 2
        K2 - K5 = 24
        K2 - K6 = 3
        K3 - K4 = 9
        K3 - K5 = 5
        K3 - K6 = 10
        K4 - K5 = 22
        K4 - K6 = 1
        K5 - K6 = 5

All 15 relative shifts agree, so the keyword is the result of some shift applied to APWNRM.

Step 4. Of the 26 possible shifts of APWNRM, only one result made sense, namely CRYPTO (or A |-> C), whose inverse produced the following plaintext:

        ilearnedhowtocalculatetheamountofpaperneededf
        oraroomwheniwasatschoolyoumultiplythesquarefo
        otageofthewallsbythecubiccontentsoftheflooran
        dceilingcombinedanddoubleityouthenallowhalfth
        etotalforopeningssuchaswindowsanddoorsthenyou
        allowtheotherhalfformatchingthepatternthenyou
        doublethewholethingagaintogiveamarginoferrora
        ndthenyouorderthepaper

Plaintext:
I learned how to calculate the amount of paper needed for a room when I was at school. You multiply the square footage of the walls by the cubic contents of the floor and ceiling combined and double it. You then allow half the total for openings such as windows and doors. Then you allow the other half for matching the pattern. Then you double the whole thing again to give a margin of error, and then you order the paper.

Ctxt: KQEREJEBCPPCJCRKIEACUZBKRVPKRBCIBQCARBJCVFCUP
Ptxt: ocanadaterredenosaieuxtonfrontestceintdefleur

      KRIOFKPACUZQEPBKRXPEIIEABDKPBCPFCDCCAFIEABDKP
      onsglorieuxcartonbrassaitporterlepeeilsaitpor

      BCPFEQPKAZBKRHAIBKAPCCIBURCCDKDCCJCIDFUIXPAFF
      terlacroixtonhistoireestuneepopeedesplusbrill

      ERBICZDFKABICBBENEFCUPJCVKABPCYDCCDPKBCOCPERK
      antsexploitsettavaleurdefoitrempeeprotegerano

      IVKSCPICBRKIJPKABI
      sfoyersetnosdroits

Step 1. Analysis:

Ordr: 0  1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Ctxt: A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  W  X  Y  Z
Freq: 13 21 32 9  13 10    1  16 6  20       1  2  20 4  12 1     6  4     2  1  4
Rank: 6  2  1  10 7  9        5  11 3              4     8        12
Ptxt: i  t  e  p  a  l  w  h  s  d  o  z  k  v  g  r  c  n  y  j  u  f  q  b  m  x

Step 2. Hypotheses:

	C --> e highest count.
	B --> t worked

Step 3. Solution:

        4a  + b = 2       ->     15a = 8    -> a = 19, b = 4
        19a + b = 10

Step 4. Expression:

Encryption: e_k(x) = 19x + 4

Decryption: d_k(y) = 11(y-4) = 11y - 44

1.1d) Unspecified Cipher

Ciphertext:

        BNVSNSIHQCEELSSKKYERIFJKXUMBGYKAMQLJTYAVFBKVT
        DVBPVVRJYYLAOKYMPQSCGDLFSRLLPROYGESEBUUALRWXM
        MASAZLGLEDFJBZAVVPXWICGJXASCBYEHOSNMULKCEAHTQ
        OKMFLEBKFXLRRFDTZXCIWBJSICBGAWDVYDHAVFJXZIBKC
        GJIWEAHTTOEWTUHKRQVVRGZBXYIREMMASCSPBNLHJMBLR
        FFJELHWEYLWISTFVVYFJCMHYUYRUFSFMGESIGRLWALSWM
        NUHSIMYYITCCQPZSICEHBCCMZFEGVJYOCDEMMPGHVAAUM
        ELCMOEHVLTIPSUYILVGFLMVWDVYDBTHFRAYISYSGKVSUU
        HYHGGCKTMBLRX

Step 1. Run the index of coincidence test, which shows that 6 could be the keyword length.

Step 2.Assuming a keyword length of 6, we produce the following 15 relative shifts:

        K1 - K2 = 12
        K1 - K3 = 15
        K1 - K4 = 5
        K1 - K5 = 2
        K1 - K6 = 21
        K2 - K3 = 3
        K2 - K4 = 19
        K2 - K5 = 16
        K2 - K6 = 9
        K3 - K4 = 16
        K3 - K5 = 13
        K3 - K6 = 6
        K4 - K5 = 23
        K4 - K6 = 16
        K6 - K6 = 19
	

All 15 shifts agree, and we find that the keyword is some shifted version of AOLVYF.

Step 3. A trial decryption that makes sense is THEORY, which produces the following trial plaintext:

        igrewupamongslowtalkersmeninparticularwhodrop
        pedwordsafewatatimelikebeansinahillandwhenigo
        ttominneapoliswherepeopletookalakewobegoncomm
        atomeantheendofastoryicouldntspeakawholesente
        nceincompanyandwasconsiderednottoobrightsoien
        rolledinaspeechcoursetaughtbyorvillesandthefo
        underofreflexiverelaxologyaselfhypnotictechni
        quethatenabledapersontospeakuptothreehundredw
        ordsperminute
	

that, when formatted, appear as:
I grew up among slow talkers. Men in particular who dropped words a few at a time like beans in a hill. And when I got to Minneapolis, where people took a Lake Wobegon comma to mean the end of a story, I couldn't speak a whole sentence in company and was considered not too bright. So I enrolled in a speech course taught by Orville Sand, the founder of reflexive relaxology, a self hypnotic technique that enabled a person to speak up to three hundred words per minute.

Problem 1.2

a) How many 2x2 matrices are there that are invertible over Z₂₆?
Ans: There are 26⁴ = 456,976 total matrices, of which 419,328 are invertible. This can be determined by the brute-force programming technique of (a) constructing each matrix then (b) trying to invert the matrices, and (c) accumulating a count of those that can be inverted. Alternatively, you can derive the number of matrices that have linear dependencies between rows and columns (a difficult task).

b) Let p be prime. Show that the number of 2x2 matrices that are invertible over Z_p is given by N = (p² - 1)(p²- p).

Ans: Since very few students got this one right, we are leaving the proof as an exercise. Taken together with the following hint, consider that the factorization of N is p(p + 1)(p - 1)².
Hint: Since p is prime, Z_p is a field. (Why?) Use the fact that a matrix over a field is invertible if and only if its rows are linearly independent vectors (i.e., there does not exist a non-zero linear combination of the rows whose pointwise sum is the zero-valued vector).

c) For p prime and m > 3 an integer, find a formula for the number of mxm matrices that are invertible over Z_p.

Ans: (p^m - 1)(p^m - p)(p^m - p²).........(p^m - p^m-1).

Problem 1.4. Suppose we are told that the plaintext

		   conversation
		   

		   HIARRTNUYTUS 
		   

Ans: Indexing the plaintext and ciphertext via the indexing function f : {A,B,...,Z} -> Z₂₆, we obtain:

	Ptxt Index:  02 14 13 21 04 17 18 00 19 08 14 13
	Ctxt Index:  07 08 00 17 17 19 13 20 24 19 20 18
	

Let gcd(detA_mxm , 26) 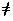1 . The following three cases suffice:

Case 1: Let m = 2 :



Case 2: Let m = 3 :



Case 3: Let m = 4 :

                c r y p
                t o g r
                a p h y
   

a) Describe how Bob would decrypt a ciphertext, given values for m and n.

Ans: To decrypt this ciphertext, with known values for m and n:
1. Partition the ciphertext into blocks of mn letters.
2. Rearrange each block in the following way:

              1 + 0*m, 1 + 1*n, 1 + 2*n, ......, 1 + (m-1)*n,
              2 + 0*m, 2 + 1*n, ..............., 2 + (m-1)*n,
                                .
                                .
                                .
              n + 0*m, n + 1*n, ..............., n + (m-1)*n
   	

3. Join the sets in sequence to obtain the plaintext.

b) Decrypt the following ciphertext, which was obtained using the preceding method of encryption:

       Ctxt: MYAMRARUYIQTENCTORAHROYWDSOYEOUARRGDERNOGW
    

Ans: First, create partitions of mn=6 (3x2) letters, as follows:

        MY AM RA      maryma
        RU YI QT      ryquit
        EN CT OR      econtr
        AH RO YW      aryhow
        DS OY EO      doesyo
        UA RR GD      urgard
        ER NO GW      engrow      
     

The formatted plaintext follows:

        Mary, Mary, quite contrary, how does your garden grow?
     

Problem 1.11. We describe a stream cipher that is a modification of the Vigenere cipher...Each time we use the keyword we replace each letter by its successor modulo 26. For example, we use SUMMER to encrypt the first six letters, then TVNNFS to encrypt the second six letters, and so forth. Describe how you can use the concept of index of coincidence to first determine the length of the keyword, then actually find the keyword. Test your method by cryptanalyzing the following ciphertext:

        IYMYSILONRFNCQXQJEDSHBUIBCJUZBOLFQYSCHATPEQGQ
        JEJNGNXZWHHGWFSUKULJQACZKKJOAAHGKEMTAFGMKVRDO
        PXNEHEKZNKFSKIFRQVHHOVXINPHMRTJPYWQGJWPUUVKFP
        OAWPMRKKQZWLQDYAZDRMLPBJKJOBWIWPSEPVVQMBCRYVC
        RUZAAOUMBCHDAGDIEMSZFZHALIGKEMJJFPCIWKRMLMPIN
        AYOFIREAOLDTHITDVRMSE

Ans: Step 1. We determine the length of the keyword by applying a shifted version of the Kasiski test. Here, we look for trigrams that have the same or similar shift relations(e.t. JIM and KJN and MLP) and compare their positions in the ciphertext. Following is the result of the modified Kasiski test where the trigrams and their shifted version repeat at least three times. The format is TRIGRAM:{position -> shift}+:

        ONR: 8 -> 0, 76 -> 19, 151 -> 12, 155 -> 24
        JED: 17 -> 0, 154 -> 8, 219 -> 8
        UZB: 28 -> 0, 114 -> 14, 118 -> 8
        KJO: 71 -> 0, 106 -> 7, 160 -> 26
        KEM: 78 -> 0, 201 -> 21, 208 -> 0
        LQD: 147 -> 0, 161 -> 24, 224 -> 23

Some of the intervals appear to be too small for the indicated shift, so we discard them. This leaves ten useful intervals, as follows:

        intervals       shift
  ONR:  68              19
        75              19

  JED:  137             8
        65              0

  UZB:  86              14

  KJO:  35              5
        54              19

  KEM:  123             21

  LQD:  14              24
        63              25

Unfortunately, this result is not terribly informative, except to indicate that the keyword length may either be 3, 5 or 7.

Step 2. We write a program shift.c to reverse the effect of shifting the key, in effect making the ciphertext same as that off a normal Vigenere Cipher encrypted ciphertext, assuming a known keyword length. Running the program for different keyword lengths, we calculate the Index of Coincidence(Ic) for each column of the modified ciphertext. For example, we first run shift.c on the original ciphertext for keyword length 5, then calculate the Ic for each of the 5 columns using the result, as follows:

                       Ic           Keyword Length
  Column  2       3      4       5       6       7       8        9
  1       0.048   0.048  0.054   0.090   0.071   0.074   0.068    0.066
  2       0.043   0.055  0.056   0.093   0.077   0.060   0.074    0.061
  3               0.059  0.054   0.095   0.067   0.069   0.053    0.058
  4                      0.051   0.115   0.072   0.060   0.066    0.064
  5                              0.100   0.065   0.063   0.055    0.086
  6                                      0.072   0.073   0.066    0.097
  7                                              0.061   0.060    0.059
  8                                                      0.082    0.070
  9                                                               0.075

This seems to indicate a keyword length of 5, since the highest values are located in column 5. (The Ic increases as the column grows, due to the smaller sample space, but at column 5 there is a significant maximum.)

Step 3. We compute the Mutual Index of Coincidence (MIc) for keyword length 5, and the result is less than clear:

        K1 - K2 = 24    MIc = 0.079686
        K1 - K3 = 18    MIc = 0.078870
        K1 - K4 = 17    MIc = 0.087644
        K1 - K5 = 22    MIc = 0.079890
        K2 - K3 = 9     MIc = 0.077051
        K2 - K4 = 5     MIc = 0.088713
        K2 - K5 = 13    MIc = 0.083715
        K3 - K4 = 3     MIc = 0.082466
        K3 - K5 = 3     MIc = 0.083090
        K4 - K5 = 23    MIc = 0.087880

It is obvious that the relative shifts don't agree with each other. Either the keyword length is not 5, or the plaintext is too small or is highly variant spatially. Trying other keyword lengths (e.g., 3, 6, or 7), yields poor results, so we use m = 5 and try combinations of relative shifts to construct keywords.

The first trial is derived from the first 4 relative shifts that have K1, namely, ACIJE, which does not work.

Step 4. We try the relative shift K2 - K3 = 9. But which of the first two relative shifts should we discard? Getting rid of K1 - K2 = 24 yields ARIJE, which didn't work either. However, keeping K1 - K2 = 24 and discarding K1 - K3 = 18 yields ACTJE.

One of the 26 decryptions started with the following characters:

        theaz stfox ousqc yptcw ogige inhwd tormz wesvt faapl esgeo
        whoeh edwot habeo whoeh esotd anreo ......

It looked like the first three letters were right, since some blocks began with: the, who, who, in, an.

Step 5. Since the relative shifts K1 - K2 and K1 - K3 and K2 - K3 are assumed to be correct, the other relative shifts had something to do with the first three letters. First K2 - K4 = 5 yields ACTXC, which didn't work. Then, we tried K2 - K5 = 13, which yielded ACTJP and gave the trial plaintext:

        theaostfomousqryptclogigtinhws

The word fomous really looked like famous, and shifting K4 by 14 matched the relative shift K2 - K4 = 5. The new keyword is ACTXP which has as one of its shifted versions PRIME.

This produced the trial plaintext:

        themostfamouscryptologistinhistoryoweshisfamelesstowhat
        hedidthantowhathesaidandtothesensationalwayinwhichhesaidit
        andthiswasmostperfectlyincharacterforherbertosborneyardley
        wasperhapsthemostengagingarticulateandtechnicolored
        personalityinthebusiness

which, when formatted, becomes:

        The most famous cryptologist in history owes his fame less to what
        he did than to what he said and to the sensational way in which
        he said it, and this was most perfectly in character, for Herbert
        Osborne Yardley was perhaps the most engaging articulate and
        technicolored personality in the business.

This concludes the solution for Homework #1, Fall 1996. If you have a solution that you'd like us to review (and possibly post on this Web page), please feel free to submit an ASCII or HTML file via E-mail to Dr. Schmalz.