Cryptology - I: Appendix A - Review of Statistics
In this class, we often express cryptologic theory in terms of statistical
measures. Since one's recall of basic statistics may require improvement in
order to follow the lecture material,
we present the following brief review. We begin with a summary of
parameters and distributions, then discuss computational means for
determining such distributions. Finally, we consider how various
distributions can be manipulated to achieve certain
properties, such as increased entropy or randomness.
A-1. Statistical Parameters.
Basic statistical parameters include the mean, standard deviation,
central and noncentral moments, as well as measures derived from
moments (e.g., skewness and kurtosis). Following preliminary
definitions, we show how certain measures can be
computed from the histogram of an image or message.
- Definition. The arithmetic mean of an image a
 RX
is given by
RX
is given by
µ(a) =
 a / |X|
a / |X|
and the standard deviation about the mean is given by:
 (a) =
(
(a) =
( (a-µ)2 / |X| )1/2 ,
(a-µ)2 / |X| )1/2 ,
which is the square root of the variance of a,
denoted by v(a) =  2.
2.
Example. If a = (1,3,2,4), then µ(a) =
(1+3+2+4)/4 = 10/4 = 2.5, since there are four elements in a.
The standard deviation
 (a) is computed
according to the following steps:
(a) is computed
according to the following steps:
- Compute the partial differences (1-2.5, 3-2.5, 2-2.5,
and 4-2.5), which yields
(-1.5, 0.5, -0.5, 1.5).
- Square the partial differences to obtain (2.25,0.25,
0.25,2.25).
- Sum the squares of the partial differences to obtain
2.25+0.25+0.25+2.25 = 5.
- Divide by |X| = 4 to obtain 5/4 = 1.25.
- Take the square root of 1.25 to obtain
 (a) = 1.18034.
(a) = 1.18034.
- Definition. The histogram of an image or message
a
 RX
is a map h
RX
is a map h  NF whose fth bin count
is given by:
NF whose fth bin count
is given by:
h(a)(f) = 
 =f (a) ,
f
=f (a) ,
f  F .
F .
Example. If a = (A,B,R,A,C,A,D,A,B,R,A) and we
denote h(A) 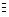 h(a)(A), then
h(A) = 5 since there are 5 A's in
Abracadabra. Additionally, h(B) = 2,
h(C) = 1, and so forth.
h(a)(A), then
h(A) = 5 since there are 5 A's in
Abracadabra. Additionally, h(B) = 2,
h(C) = 1, and so forth.
Algorithm. If a
 (Zn)X, then
the histogram h(a) can be computed as:
(Zn)X, then
the histogram h(a) can be computed as:
h := 0
for each x in X do:
{ h(a(x)) := h(a(x)) + 1 } .
The resultant histogram will have n bins.
Observation. The histogram h(a) can be used
to compute the image mean µ and variance
 2 of
image a, as follows:
2 of
image a, as follows:
µ(a) =
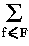 f · h(f) / |X|
f · h(f) / |X|
 2(a) =
2(a) =
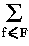 (f-µ)2 · h(f) / |X| .
(f-µ)2 · h(f) / |X| .
Remark. It is appropriate to think of a histogram as a
distribution of frequency-of-occurrence. Note that a frequency
distribution h(a) is proportional to a
probability distribution Pr(a),
since Pr(f) = h(f) /
 h, where
f
h, where
f domain(h).
Alternatively, we can say that
f
domain(h).
Alternatively, we can say that
f range(a),
which implies that
range(a),
which implies that
Pr(a) = h(a) /
 h .
h .
The preceding summation operation can be thought of in terms of
Reimann-Stiltjes integration, versus Lebesque integration where
Pr(f) = h(f) /
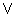 h.
For example, via Lebesque integration, h(a) could
be normalized to the unit interval
[0,1]
h.
For example, via Lebesque integration, h(a) could
be normalized to the unit interval
[0,1] R to yield
the following distribution of the values of a:
R to yield
the following distribution of the values of a:
Pr(a) = h(a) /
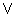 (h) .
(h) .
These techniques for constructing a probability distribution from
the image (message) histogram will be useful for attacking
encryptions that disclose
part or all of the plaintext histogram in the corresponding
ciphertext.
- Definition. Given an image a
 RX,
the first two central moments of the histogram
h(a) are defined as
RX,
the first two central moments of the histogram
h(a) are defined as
m1(h) = µ and
m2(h) =
 2 ,
2 ,
where µ and  were
defined in the preceding Observation.
The kth central moment of the histogram h of an
image a
were
defined in the preceding Observation.
The kth central moment of the histogram h of an
image a  FX is given by:
FX is given by:
mk(h) =
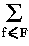 h(f) ·
(f-µ(h))k / |X| .
h(f) ·
(f-µ(h))k / |X| .
Remark. Histogram moments are often employed as measures of
probabilistic dispersion. In contrast, moments of an image
defined over a spatial domain X characterize the
spatial dispersion of the image. In the former case, we are
concerned with frequency-of-occurrence.
The latter (spatial) case is related to global
analysis of shape or morphology, which is not emphasized in this
class. Thus, the histogram's kth moment
mk(h) should not be confused with the
kth moment mk(a) of the
corresponding image (or message), which is given by
mk(a) =
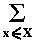 a(x) · xk / |X| .
a(x) · xk / |X| .
For example, Figure A-1(a) illustrates the spatial mean
or centroid m1,1(a)
of a sickle-shaped object in an image, while
Figure A-1(b) shows the mean of a histogram that could be
derived from an image similar to a that has ten greylevels.
In Figure A-1(b), it is a coincidence only that the mean falls
within the histogram bin which is the mode, or
most frequently occurring value.
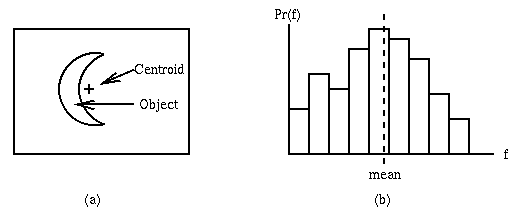
Figure A-1. (a) Spatial mean (centroid) of
an object in an image defined on a two-dimensional
domain; (b) Mean of a histogram.
- Concept.
In cryptology, instead of thinking in terms of spatial moments,
we typically analyze message statistics, such as the mean and
mode values, as well as moments of plaintext and ciphertext
histograms. We also examine co-occurrence of text, which can
be quantified in terms of a histogram.
For example, consider that n adjacent symbols denoted by
s = (s1,s2,...,sn),
which is often called an n-gram, has a probability of
occurrence Pr(s) within a given text corpus. Such simple
observations are the basis for the Hill cipher, which we will
discuss later in this class, as well as for effective attacks upon
a wide variety of encryptions. We thus consider several measures
or parameters that can be derived from a histogram.
Observation. When conducting statistical cryptanalysis,
one often needs to know when a value in plaintext or ciphertext
occurs frequently. In particular, we would like to know the
value that occurs most frequently, which is called the mode.
Definition. Given an image a
 FX,
the mode of a is computed
from the histogram h(a) as
FX,
the mode of a is computed
from the histogram h(a) as
mode(a) = domain(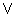 h) .
h) .
Definition. A distribution that has one (more than one) peak
or local maximum is called monomodal (multimodal).
Observation. For similar reasons, we would like to know
the partition of domain(h) that divides lesser
values (which, taken together, occur 50 percent of the time) from
values greater than the partition. The partition value is
called the median, which is computed from the cumulative
histogram. The following definitions apply.
Definition. Given an image a
 FX,
the cumulative histogram c(a) is computed
recursively from the histogram h(a) as follows.
Let F be indexed by i
FX,
the cumulative histogram c(a) is computed
recursively from the histogram h(a) as follows.
Let F be indexed by i {1,2,...,|F|} such that there are no values in F between
fi-1 and fi, where fi-1 <
fi. Then, we have
{1,2,...,|F|} such that there are no values in F between
fi-1 and fi, where fi-1 <
fi. Then, we have
[c(h)](fi) =
[c(h)](fi-1)
+ h(fi) .
Definition. Given an image a
 FX
and its cumulative histogram c(a), the median
of a is given by
FX
and its cumulative histogram c(a), the median
of a is given by
median(a) = 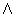 (domain(c || > |X|/2))
(domain(c || > |X|/2))
Algorithm. Given an N-pixel image (or N-character message)
a FX and its histogram h
FX and its histogram h NF, the mode and median of
a are computed from the cumulative distribution
c
NF, the mode and median of
a are computed from the cumulative distribution
c NF, as follows:
NF, as follows:
c(f1) := h(f1)
freq := 0
notm := 1
for each i from 2 to |F| do:
{ c(fi) := c(fi-1) + h(fi)
if (h(fi) > freq) then
{ mode := fi
freq := h(fi) }
if (notm AND c(fi) > |X|/2) then
{ median := fi
notm := 0 } } .
A-2. Computing Probability Distributions.
In this section, we discuss the nature and computation of various
types of probability distributions (e.g., Gaussian, Poisson, Lorentzian,
Gamma, Chi-squared, and Student's t) that will be useful in cryptanalysis.
As an example, we present theory and algorithms for the Gaussian
distribution. In Section A-3, we discuss the manipulation of such
distributions as a prelude to statistical cryptanalysis.
There are many different types of probability distributions, each
of which has been derived from observations of natural phenomena.
Unfortunately, common probability distributions are rarely derived from
first principles. That is, the laws of physics are typically not
employed to construct a body of theory from which a given distribution
is computed a priori. Rather, data is gathered from observations of
one or more processes, and a probability distribution is fitted to
measures derived from the data. Thus, in practice, there are relatively
few causal models that can deterministically link a given
physical process with the statistical distribution that characterizes
the outcomes of that process. As a result, one often has little knowledge
about why a given distribution occurs in a given situation.
For example, it is well known that the times between arrival of photons
at a detector
can be characterized with reasonable accuracy by a Poisson distribution.
It is likewise known that the greylevels of images that depict
natural scenes under spatially uniform illumination are typically
Gaussian-distributed.
Lettington [Let94] has shown that the greylevels of gradient images taken
from selected scenes that contain naturally-occurring or manufactured
objects generally conform to a Lorentzian distribution. The reasons
for these behaviors are presently not apparent. As a result, there are
interesting possibilities for research in causal models that
underlie probability distributions.
- Definition. A sample space is the set of all
possible outcomes of a given process.
Example. Given B = {0,1} and a process P:
B2 -> B2, the set of all
possible outcomes is B2 = {(0,0),(0,1),(1,0),(1,1)}.
Definition. A probability measure on a set S is
denoted by Pr: 2S -> [0,1], such that the following
conditions are satisfied:
- Pr(Ø) = 0, Pr(S) = 1; and
- If A,B
 S are
disjoint, then
S are
disjoint, then
Pr(A 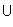 B) =
Pr(A) + Pr(B) .
B) =
Pr(A) + Pr(B) .

 (I)
(I)
Definition. An event is a subset of a sample space.
Example. E = {a,c} is an event in a sample space S = {a,b,c}.
Definition. Given an event E in sample space S,
and another event E´ that is the complement of E, the
following statements hold:
- E´ = S \ E .
- Pr(E´) = 1 - Pr(E).
Statement 2 follows from the fact that S is the disjoint union
of E and E´. Thus, from (I), we have 1 = Pr(S) = Pr(E) +
Pr(E´).
Lemma. If events A,B  S are non-disjoint, then
S are non-disjoint, then
Pr(A 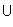 B) =
Pr(A) + Pr(B)
- Pr(A
B) =
Pr(A) + Pr(B)
- Pr(A 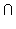 B).
B).

 (II)
(II)
Proof. The proof, which is left as an exercise,
could appear as homework.
Example. Given a sample space S = {a,b,c,d}, let
A = {a,b} and B = {b,c}, with Pr(a) = Pr(b) = Pr(c) = 1/4. Let
Pr(A) = Pr(B) = 0.3. Since
A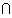 B = {b}, we have
B = {b}, we have
Pr(A 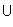 B) = Pr({a,b,c})
= Pr(A) + Pr(B) - Pr(A
B) = Pr({a,b,c})
= Pr(A) + Pr(B) - Pr(A 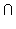 B)
B)
= 0.3 + 0.3 - 0.25 = 0.6 - 0.25 = 0.35 .
Lemma. If events A,B  S are conjoint (i.e., occur together), then
S are conjoint (i.e., occur together), then
Pr(A 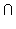 B) =
Pr(A) · Pr(B)
B) =
Pr(A) · Pr(B)
Definition. Given a sample space S with subsets
A and B that have nonzero probabilities, the conditional
probability of B on A (also called the probability
of B given A) is given by
 Pr(A
Pr(A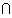 B)
B)
Pr(A|B) =  .
.
 Pr(A)
Pr(A)
Definition. Given events A,B S, if A and B are independent, then the
following statements hold:
S, if A and B are independent, then the
following statements hold:
- Pr(A
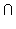 B) =
Pr(A) · Pr(B), and
B) =
Pr(A) · Pr(B), and
- Pr(B|A) = Pr(B).
Definition. If A and B are any events in a sample
space S, then
Pr(A 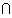 B) = Pr(A) · Pr(B|A) .
B) = Pr(A) · Pr(B|A) .
Note the difference between the preceding two definitions, which
specify probabilities for independent versus general events.
Remark. The concept of probability assumes that all
possible outcomes can be specified within a given sample space.
In finite discrete systems such as cryptosystems, this constraint
of a priori omniscience is usually not problematic, since
all outcomes of a finite process can be enumerated in finite time,
given finite resources. However, in continuous physical models,
the definition of probability is somewhat tenuous since the
outcomes of nontrivial infinite processes that occur in an infinite
system generally cannot be determined in finite time with finite
resources. In this class,
practical applications of probability theory emphasize finite,
discrete processes and their corresponding distributions. Thus, we
address only infrequently those issues pertaining to continuous
versus discrete systems.
- Definition. A random variable on F
is a map X: F -> R. The probability that
X takes the value c for outcomes s
 S is expressed as:
S is expressed as:
Pr(X=c) = Pr({s S :
X(s) = c}) .
S :
X(s) = c}) .
Symmetric statements hold for inequality relations such as less-than
(<) and greater-than (>).
Definition. If X is a random variable on a sample
space S with probability measure Pr, then a probability
distribution f associated with X is defined as:
f(x) = Pr(X = x) .
Remark. In this class, we restrict the preceding definition
to describe a probability distribution on a finite discrete set
F as a map d: F -> [0,1].
Definition. A trivial process is one that has the
same outcome for all inputs.
Example. Multiplication by zero or one are trivial processes
over the real numbers.
Definition. A uniformly random process has a
probability distribution that is a constant image.
Observation. Given a finite, discrete process a
 FX
where a has equiprobable values, the distribution
Pr(a) can be expressed as
FX
where a has equiprobable values, the distribution
Pr(a) can be expressed as
Pr(f) = 1/|F|, 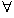 f
f F .
F .
In practice, we can write the preceding statement more generally
as Pr(a) = 1/|range(a)|.
Example. If a = (A,B,A,C,C,B), then F =
{A,B,C} and Pr(F) = 1/|F| = 1/3.
- Observation. A uniformly random distribution can be thought
of as a trivial mapping, since the outcome is the same for every
input value. Later in this class, we shall see that such
distributions can be said to have near-zero information content,
because they can be characterized by at most one bit that indicates
randomness or nonrandomness. As the domain size |X|
approaches infinity, one can say that the amount of information
per symbol which a given uniform distribution conveys approaches
an asymptotic limit of
1/|X| = zero bits. If the domain of a discrete distribution
(i.e., a symbolic alphabet F) is finite, then the alphabet size
|F| can be derived from the distribution, since all values
of the distribution equal 1/|F|. Thus, there can be said
to exist at most one bit of useful information in a uniform
distribution.
Remark. The preceding expression has a dual
information-theoretic representation that defines the entropy
(disorder)
in a random process. For example, if a sample space S can be
encoded in a maximum of m bits, then the entropy of each element
of S is m bits. That is, if d is a random process over
an alphabet S, then the minimum possible
entropy for the encoding of each symbol in S by d is m bits.
Thus, each
input element of d is represented by no fewer than m
bits.
While it may seem that the preceding statement contradicts the
observation that the information-theoretic content of a given
distribution can be expressed in terms of one bit, there
exists no such contradiction in practice.
Since we will shortly provide a proof sketch to the effect that
random distributions cannot
occur over finite discrete sets, this is (in practice) a moot
point. However, such arguments serve to highlight two issues:
- In many mathematical representations (including information
theory) a statement may have a dual expression that describes the
same statement in a different way. As a familiar example, consider
deMorgan's Laws.
- The information-theoretic description of complete randomness
remains somewhat ambiguous. Thus, as you read through the
literature of cryptology, and as we consider various topics in
this class, bear in mind that much development remains in the
various areas of mathematics which we discuss herein.
Digression. Since uniformly random entities or distributions
have zero information per symbol at the asymptotic limit, there have
been posed several questions regarding the physical and philosophical
basis for the existence
of processes in the natural world that have equiprobable outcomes.
We discuss this issue briefly, since it is germane to several
practical topics in key generation and cryptanalysis. For example,
assume (for purposes of argument) that a purpose of physical
existence is the achievement of non-randomness. By this definition,
a uniformly random distribution could not exist physically.
Similarly, if the purpose of existence is to convey information,
then uniform randomness would convey zero information at the
aforementioned asymptotic limit. As a result, one can say that
the aforementioned precondition
for existence has been violated. Since the purpose of existence is
not known in the philosophical sense, these arguments may
properly be viewed as moot.
An alternative conjecture derives from physics, where
the Second Law of Thermodynamics (STL) states that global entropy
(a measure of disorder) can only increase with time. For example,
if the Universe was completely randomized, then its entropy would
be maximized and could not increase further. This could,
in principle, violate the STL. Likewise, the STL implies
that the entropy of a local reference frame that is isolated
from the rest of the Universe can only increase. (By "isolated"
we mean that no energy is transferred into or out of the reference
frame.) By the preceding argument, such completely random, local,
such isolated processes could (in principle) violate the STL.
The preceding conjecture is interesting but trivial, since
(a) the Universe is not everywhere random at all spatial scales
and (b) we
do not know how to produce random isolated processes. At a
practical level, however, it follows that questions should arise
concerning the security of
"random" key sequences using methods such as radioactive decay,
quantum fluctuations in photodetectors, etc. We shall address
such questions later in this section. For now, it suffices
to state the following theorem.
Theorem. No nontrivial finite, discrete process can
have equiprobable outcomes (i.e., have a sample space whose elements
are uniformly distributed.)
Proof. We outline the proof as follows.
First, note that uniform distribution
implies an equiprobable measure. Second, note that every
finite discrete system can be mapped to Z+.
Now, it is well known that there exists no equiprobable measure
on the positive integers, since no probability, however
small, can represent the probability of choosing an integer.
In particular, if p denotes a vanishingly small probability, then
there exists some positive integer n for which Pr({1,2,...,n})
= np > 1. The net probability is given by the probability
of each integer (p) times the number of integers from 1 to
n, per Equation (I), above. 
Remark. The formal proof could be assigned on an exam
or as homework.
-
Question. Why study random distributions, especially
if they do not exist in finite, discrete systems?
Remark. Interestingly enough, the computation of uniformly
random distributions remains one of the key goals of number theory
and cryptology. The use of randomness to obscure properties
of a message that are useful to a cryptanalyst
(i.e., an adversary) is a key problem in existing cryptographic
theory and practice. Therefore, we emphasize discussion
of various techniques for computing "uniformly random"
distributions from nonrandom processes or data.
Later in this class we will consider the problem of semantic
ciphers or steganography, in which properties of
plaintext are disguised in the ciphertext so as to appear innocuous.
In the absence of techniques for rigorously producing random processes,
such camouflage methods may be a more operationally feasible approach
to disguising plaintext than attempting to simulate randomness.
Observation. One needs random bits (or values) for several
cryptographic purposes, of which the two most common are (a)
generation of cryptographic keys (or passwords) and (b) concealment
of values in certain protocols. Several definitions of randomness
are employed in cryptology. However, there is the following basic,
implementational criterion for a random source.
Assumption. Let an adversary have
(i) full knowledge of an encryption site's software/ hardware,
(ii) the money to build and run a matching cryptosystem for
exhaustive attack, and (iii) the ability to compromise the site's
physical facilities (i.e., wiretapping, planting bugs, etc.)
This capable adversary must not be able to predict the next bit
the site's "random" generator produces, even if he knows all the
bits produced at the site thus far.
-
Definition. Implementationally, random sources can be
classified as random or pseudo-random. Since we
have shown that no discrete system can be random, the random
number (RN) generation techniques we shall discuss are algorithms
or physical processes that imitate true randomness. Random sources
can be considered unconditionally unguessable, even by
an adversary with infinite computing resources. In contrast,
pseudo-random sources useful only in the presence of attacks
constrained by finite computational resources.
Observation. Random bits are typically obtained via the
following process:
- Gather a physically-generated bitstream.
One first gathers bits unknown to and unguessable by the adversary.
Such information is typically generated by a high-entropy
(nearly random) physical device connected to one's
cryptographic equipment by a secure I/O line. For example, the
following techniques have been suggested or employed:
- Radioactive Source that emits particles to a
completely absorbing counter. The counter must be absorbing
in order to conceal the bitstream. Several commercially
available radioactive monitors have RS232 output. Hence, this is
a practical method.
- Quantum Effects in Semiconductors (e.g., noisy diodes).
Several electronic sources of nearly-random bitstreams use noisy
diodes or
noisy resistors, which can be cost effective. As in the case of
a radioactive source, the semiconductor must be completely
shielded.
- Photon Polarization Detection This is a source of
quantum uncertainty that is highly experimental,
and will be discussed later in this class.
- Isolate Monoaural Microphone In some cases,
an analog-to-digital
converter whose input is an unplugged microphone yields noise that
exhibits moderate entropy levels.
Note that the microphone input must be fully
shielded to avoid corruption by correlated (real-world) sounds
such as voice, keyboard clicks, 60Hz electrical hum, etc.
- Air Turbulence within a Dedicated Sealed Disk Drive
has been reported recently [Dav94]. This mechanism shows
promise, given a dedicated secure disk drive and special system
software to measure disk performance parameters without affecting
disk behavior. If a non-dedicated drive and customary software
are employed, then one can measure I/O completion times for a
disk in normal use, which are known to be Poisson-distributed.
However, this method does not hold if the disk drive is not
properly balanced or is defective, since correlated noise can
result, for example, from spindle "tramping" due to mechanical
imbalance.
Additional methods for producing random bits that
yield pseudorandom output include:
- Differenced Stereo Microphone Output, where a noisy
room with moving sound sources can yield stereo disparity between
two microphones that fluctuates pseudorandomly. If the microphone
amplification is normalized to minimize the difference signal,
it is difficult for an adversary to reconstruct the resultant
bit stream, whether or not the room is bugged with a monoaural
microphone. If the room is bugged with a stereo
microphone, or is a realistic environment having correlated
signals, then this method is highly vulnerable to correlations
between noise detected by the adversary and noise used to generate
the bitstream.
- Monaural Microphone in a secure (unbugged)
room can detect certain random signals. However, the randomness
will be submerged in a large amount of correlated noise.
Additionally, one cannot guarantee if the room is bugged.
- Timing between Keystrokes, where a user types nonsense
and the key value and activation time are collected.
Keying times are quantized by the system clock, thus requiring
predictive modelling of expected inter-keying delay and
quantization error
values for each implementation. Due to temporal quantization,
such systems are insecure within several orders of magnitude
greater than the temporal quantization interval. For fast
typists, this constraint may be prohibitive. Additionally,
unshielded keyboards or audio listening devices placed in the
room that contains the keyboard can facilitate
compromise of this method.
- Mouse Stroke Timing, derived from a user signing
his name with a mouse or joystick. Although this is
likely the most efficient human-driven sources of entropy
it can be easily compromised by poorly shielded equipment
or bugs placed within the mouse pad.
- /dev/random is a UNIX device
available on certain secure systems that gathers bits from system
tables and events unavailable to users. If the adversary is a
user running a process on your machine, the source remains
secure. If an adversary has certain system privileges,
then the method can be easily compromised.
The following methods are often used as bit sources, but have
serious flaws since they are observable, predictable, or subject to
influence by a determined adversary, especially on multiprocess
machines:
- Network Statistics can easily be influenced
by a capable adversary with communication-intensive software.
- Process Statistics are less easily influenced, but can
be easily compromised by determined adversaries executing
concurrent heterogeneous processes.
- I/O Completion Timing and Statistics are readily
influenced by I/O-intensive processes run by an adversary.
The following are nearly worthless bit sources that are frequently
recommended or used for purposes of convenience:
- TV or Radio Broadcasts are of little value, since
the majority of information not contained in local noise
is available to an adversary.
- Published Information on a CD, Tape, or Hardcopy is
vulnerable due to wide availability. An exception is a one-time
encoding on a CD of a pseudorandom bitstream in the least significant
bit of the soundtrack. This technique will be further discussed in
the section on steganography.
- System Date and Time have low information content and
are available to an adversary.
- Process Runtime has little information content except
on extremely busy systems, where adversarial influence of the
process load can corrupt the security of this measure without
necessarily being detected by security monitors. Furthermore,
the runtime calculator will, in a round-robin scheduler, make the
call to compute the runtime at an approximately uniform time after
process startup. This renders the runtime I/O measures
predictable by an adversary, especially if he can influence the
process mix.
- Multiple, Free-running Cascaded Oscillators yield a
sequence that appears to be random due to its multi-period
beat frequencies, but can easily be discerned as periodic
through application of the Fourier or Cosine transform.
Equally or entirely worthless are the following bit sources:
- Chaotic Systems appear visually complex but
are highly structured (i.e., are pseudorandom). Current research
emphasizes determination of this structure.
- System Library Random Number Generators (RNGs) were
never designed to be cryptographically strong and hence have
little utility in cryptology.
- Linear-congruential RNGs - the simplest RNG algorithm,
which we will analyze later in this class.
- Chain Addition - another simple and easily broken
statistical RNG.
-
- E-mail is useful only if the e-mail is so well encrypted
that it cannot be discovered by the adversary. In such cases,
however, one would already have an effective RNG in place. Generally,
E-mail is as vulnerable as USENET data.
Unfortunately, the bits gathered from the foregoing methods are
not necessarily independent. That is, one might be able to
predict a bit value with probability greater than 1/2, given
all other bits. The adversary might even know entire subsequences
of a bitstream, which he could obtain by eavesdropping.
The key constraint
is that the gathered bits contain information (entropy)
that is everywhere unavailable to the adversary.
- Determine entropy by estimating how many unguessable
bits were gathered. Here, one needs to know how many of the
bits are independent and unguessable. This number of bits
is usually referred to as source entropy. We will discuss
this concept in greater depth when we consider information theory
in Appendix C.
- Reduce to independent bits. As a third step, one can
hash the harvested bits to reduce them to independent random bits.
The hash function for this stage of operation needs to have each
output bit functionally dependent on all input bits but
independent of all other output bits. Without presenting
formal analysis at this time, we assume that such hash functions
are cryptographically strong. Strong hash functions such as MD5
and SHA will be discussed later in this class.
Provided that the hash function meets the required criteria and
cannot be guessed by the adversary, the output of Step 3 is a set
of independent, "unguessable" bits. These can be used with
confidence wherever random bits are required.
Remark. When implementing the foregoing method of random
number generation, one preserves security by:
- Testing bit sources for degeneration - if a bit
source becomes less random but feeds a cryptographically strong
function f, the output of f would not immediately
be problematic to the normal user but could facilitate entry to the
cryptanalyst. One needs to frequently test the bit source
[Mau91] before it is hashed.
- Mix different sources if one is unsure about tapping
or bugging. If multiple sources are used, but tapping of any
source is a probabilistically independent event, then one can
reduce the probability that a tap is successful by using multiple
independent sources. Each source would have its own bit gathering
procedure, and the individual bitstreams would be hashed together.
The probability of adversary success is then the product of the
individual probabilities of tapping. Clearly, if one source has
zero tapping probability (i.e., is secure), then the hashed bits
are secure.
- Avoid discarding known bits but feed all bits to the
initial hash function. Given a cryptographically strong hash
function, there is no other effective method for
filtering out dependent bits.
- Definition. Various types of non-uniform distributions
will be useful to us in forthcoming development. For purposes
of consistency, we assume that µ denotes the mean,
 denotes standard
deviation, and X denotes a random variable. Note that
Pr(X=x) could be computed for a uniform
distribution using the preceding method.
denotes standard
deviation, and X denotes a random variable. Note that
Pr(X=x) could be computed for a uniform
distribution using the preceding method.
- Normal Distribution: A discrete random variable X
that is normally distributed has a probability function given by
 e-(x - µ)2/2
e-(x - µ)2/2 2
2
Pr(X=x) = 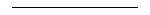 .
.

 ·(2
·(2 )1/2
)1/2
- Algorithm. Given a random number generator that
yields x
 [-q,q],
where q is a multiple of
[-q,q],
where q is a multiple of  ,
we can compute Pr(x) according to the normal distribution,
as follows:
,
we can compute Pr(x) according to the normal distribution,
as follows:
normal(x,mean,stdev):
{ pi := 3.14159
den1 := 2*stdev^2
den2 := stdev*sqrt(2*pi)
coef := -(x - mean)^2/(2*den1)
prob := exp(coef)/den2
return(prob) } ,
where stdev denotes standard deviation.
- Poisson Distribution: If µ > 0 and x
 N, then the
Poisson-distributed discrete random variable X
has a probability function given by
N, then the
Poisson-distributed discrete random variable X
has a probability function given by
 e-µ · µx
e-µ · µx
Pr(X=x) = 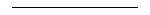 ,
,
 x!
x!
where  2
= µ. Since X can be indexed by Z, the integral
constraint on x is not problematic.
2
= µ. Since X can be indexed by Z, the integral
constraint on x is not problematic.
- Gamma Distribution: The discrete random variable
X is said to be Gamma-distributed when X has a
probability function given by:
 1
1
 Pr(X=x) =
Pr(X=x) =  · xae-x/b,
· xae-x/b,

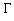 (a + 1)ba+1
(a + 1)ba+1
where 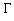 (a+1) = a!
for a,b > 0. The mean is given by µ = b(a + 1) and
the standard deviation
(a+1) = a!
for a,b > 0. The mean is given by µ = b(a + 1) and
the standard deviation  = b(a + 1)1/2.
= b(a + 1)1/2.
- Lorentzian Distribution: The discrete random variable
X is said to be Lorentzian- distributed when X has a
probability function given by:


 Pr(X=x) =
Pr(X=x) = 


 ·(x2 +
·(x2 +  2)
2)
where  denotes the
key parameter of the distribution. For small
denotes the
key parameter of the distribution. For small
 the distribution is
sharply peaked, which effect decreases inversely with
the distribution is
sharply peaked, which effect decreases inversely with
 .
.
- Sampling Distributions: A random sample is
selected from a population in which:
- The form of the probability function is known, and
- A function of the random variables, called the sampling
distribution, is derived from the joint density of the
random variable.
We next present two commonly-used sampling distributions, whose
applications are discussed in Section A-3.
We shall next discuss uses of sampling distributions.
A-3. Manipulating Probability Distributions.
It is occasionally useful to test whether or not there is a
significant difference between two sample means. Also, we often
need to test whether two variables in a given bivariate sample
are associated with each other. For example, one might want to
test the frequencies of occurrence of digrams in plaintext and
ciphertext corpi that appear to be associated with each other.
In this section, we examine several simple but useful tests,
such as the t-test, chi-squared test for dependence, the
Phi test for association, Cramer's V-test, and Pearson correlation.
A-3.1. t-test for Significant Difference of Means.
- Observation. Probability distributions can have one or
two tails. For example, the Lorentzian (Poisson) distribution,
shown schematically in Figure A-2(a), is said to be two-tailed
(one-tailed).
Figure A-2. (a) One-tailed distribution;
(b) two-tailed distribution.
Remark. In computing the t-test, which determines if
there is a statistically significant difference between two
sample means, we must know a priori if we have a one- or
two-tailed distribution. This can be determined by examining
the histogram of the source data. Alternatively, we can fit
various known distributions to the data using a method such as
least-squares regression. The goodness-of-fit criterion will
determine which distribution best characterizes the data, and
since it will be known a priori whether or not the best-fit
distribution has one or two tails.
Concept. The t-test requires that we know the
population sizes, means, and standard deviations of two samples.
We also must know the number of tails on the distribution that
best fits the two samples, and the level of statistical signficance
at which we want to perform the t-test. Given a table of
t-distribution values (reference Equation III, above), we compute
the t-score, then look it up in the table for a given number of
tails and the predetermined level of significance. If the
entabulated t-score is less than the computed t-score, then the
difference of means is significant at the prespecified level of
significance.
Algorithm. Given random variables X and Y
represented by samples A1 and A2, perform
the following steps:
Step 1. Compute the histograms h1
and h2 from A1 and A2,
and compute the means µ1,µ2 and
standard deviations
 1,
1,
 2 from
h1 and h2, as we
showed previously. Let population sizes N1 =
2 from
h1 and h2, as we
showed previously. Let population sizes N1 =
 h1
and N2 =
h1
and N2 =
 h2.
h2.
Step 2. Compute the standard error of the difference
as follows:
 =
(
=
( 12/N1 +
12/N1 +  22/N2)1/2 .
22/N2)1/2 .
Step 3. Compute the t-score as:
t = (µ1 - µ2) /
 .
.
Step 4. Given the level of significance
0 > k < 1 and T, the number of tails on distribution
that best portrays A1 and A2, compute
the effective population size
N' = N1 + N2 - 2 ,
and look up the minimum significant t-score
tmin in a table of t-distribution values, with
k, T, and N' as table lookup constraints.
Step 5. If t > tmin, then the difference
between µ1 and µ2 is significant
at probability 1-k.
Example. If X and Y have means and standard
deviations µ1 = 70, µ2 = 60, and
 1 = 6,
1 = 6,
 2 = 8, with
population sizes N1 = N2 = 14, then
2 = 8, with
population sizes N1 = N2 = 14, then
 =
(62/14 + 82/14)1/2
=
(62/14 + 82/14)1/2
and
t = (µ1 - µ2) /
 =
(70-60)/2.67 = 3.74 .
=
(70-60)/2.67 = 3.74 .
Letting
N' = N1 + N2 -
= 14 + 14 - 2 = 26,
we look up the t-distribution entry for k = 0.05, T = 2,
and N', and find tmin = 2.056.
Since
t > tmin, the difference between
µ1 and µ2 is significant
with probability 1-k = 0.95.
Remark. If N1 + N2 < 30, then
the t-distribution table must be employed. Otherwise, the
two-tailed t-distribution approximates the normal (Gaussian)
distribution, and the latter can be used to predict the
minimum t-score. We recommend that one use the t-table
wherever possible, to achieve accuracy.
Observation. In cryptologic practice, the t-test is useful
for comparing the distribution of results between two experiments.
For example, one might correlate the histograms of various messages
in a corpus C of ciphertext with two histograms that characterize
the distribution of characters in known plaintext corpi D and E.
That is, one asks if there is a significant difference between
the distribution of correlation coefficients (results) from
the correlation f[h(m),h(D)],
m C, versus the
correlation f[h(m),h(E)]. One can apply the
t-test to the respective histograms of the correlation coefficients
to determine whether or not the histogram means are significantly
different. Although not a definitive test, such methods are useful
for introductory cryptanalysis of data that have a near-normal
distribution.
C, versus the
correlation f[h(m),h(E)]. One can apply the
t-test to the respective histograms of the correlation coefficients
to determine whether or not the histogram means are significantly
different. Although not a definitive test, such methods are useful
for introductory cryptanalysis of data that have a near-normal
distribution.
A-3.2. Chi-Squared Test for Dependence.
Unlike the t-test, which compares group means between two samples, the
chi-squared test examines nominal or ordinal measurements to compare group
frequencies. This comparison of frequency data contrasts with the t-test,
which compares means of samples that are distributed across a real-valued
interval. Thus, the chi-squared test is inherently useful in conjunction
with histogram-based manipulation.
- Concept. The chi-squared test determines independence
among two or more variables by examining whether the observed
frequencies in a sample differ significantly from
theoretical or expected frequencies.
Mathematical Description. Let a bivariate table consist
of N cells. For purposes of simplicity, we use a 2 × 2-cell
bivariate histogram h(x,y), shown in Figure A-3. It
follows that N = 2(2) = 4 cells.
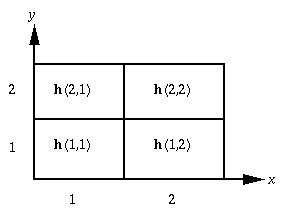
Figure A-3. Chi-squared test - 2 × 2 bivariate
histogram h.
Let fo(x,y) denote the observed frequency in each cell
and let fe(x,y) denote the expected frequency. Then,
the chi-squared score is given by
 2 =
2 =
 x
x
 y
(fo(x,y) - fe(x,y))2 /
fe(x,y) .
y
(fo(x,y) - fe(x,y))2 /
fe(x,y) .
 (IV)
(IV)
Given the degrees of freedom and the number of tails in the
best-fit distribution (as discussed in Section A-3.1)
one finds the
 2 score S
for a given level of significance 0 < k < 1 in a
2 score S
for a given level of significance 0 < k < 1 in a
 2 table
or from the
2 table
or from the
 2 distribution
(reference Section A-2). If the table or distribution result
2 distribution
(reference Section A-2). If the table or distribution result
 2 < S, then
there is no statistically significant difference between
the two entabulated variables (shown in Figure A-3).
2 < S, then
there is no statistically significant difference between
the two entabulated variables (shown in Figure A-3).
Algorithm. Let X and Y denote finite, discrete
random variables whose values are respectively indexed by the sets
U and V. Let the histogram h :
U × V -> N have N = |U| ·
|V| cells. The independence of X and Y
is tested as follows:
Step 1. Compute row and column totals of h
as:
ru =
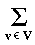 h(u,v) ,
u
h(u,v) ,
u U
U
cv =
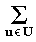 h(u,v) ,
v
h(u,v) ,
v V.
V.
Step 2. Compute the expected value
for h(u,v) as:
fe(u,v) =
(ru · cv) /
 h .
h .
Step 3. Apply Equation (IV) to yield the chi-squared
score, as follows:
 2 =
2 =
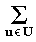
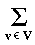 (h(u,v) -
fe(u,v))2 /
fe(u,v) .
(h(u,v) -
fe(u,v))2 /
fe(u,v) .
Step 4. Compute the degrees of freedom
d = (|U| - 1) · (|V| - 1)
and determine the number of tails T = 1 or T = 2.
Step 5. Given a prespecified confidence level 0 < k < 1,
set k' = k/|T - 3|.
Thus,
k' = k/2
for a one-tailed distribution. Given a
 2 table
or distribution, if
2 table
or distribution, if
 (d,T,k
(d,T,k') >
 2(h),
then the random variables X and
Y are not significantly different in the sample portrayed
by h. Otherwise, the variables are significantly different.
2(h),
then the random variables X and
Y are not significantly different in the sample portrayed
by h. Otherwise, the variables are significantly different.
Example. %%%TBD%%%
Remark. There are four assumptions or constraints associated
with the use of  2
testing, as follows:
2
testing, as follows:
- Individual observations that comprise the histogram h
must be mutually independent and can be represented only
once in h;
- The data are limited to frequency-of-occurrence data;
 fe
must equal
fe
must equal
 fo; and
fo; and
- If N
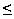 2 × 2 and
d = 1, then
2 × 2 and
d = 1, then
 2
is erroneous and requires the following correction:
2
is erroneous and requires the following correction:
 2 =
2 =
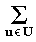
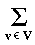 (|h(u,v) -
fe(u,v)| - 0.5)2 /
fe(u,v) ,
(|h(u,v) -
fe(u,v)| - 0.5)2 /
fe(u,v) ,
which is called the Yates correction.
A-3.3. Phi Test of Association.
Occasionally, one prefers to compare finite sets of Boolean data. The Phi
coefficient measures the association between bivariate data described by a
2 × 2-cell table. Phi is preferred over the
 2 test because Phi
corrects for the fact that the
2 test because Phi
corrects for the fact that the
 2 result varies with the
number of cases.
2 result varies with the
number of cases.
- Algorithm. Let
 2 denote the
result of the chi-squared test applied to a 2 × 2 table of
bivariate Boolean data compiled from N test cases. The
Phi test result is given by:
2 denote the
result of the chi-squared test applied to a 2 × 2 table of
bivariate Boolean data compiled from N test cases. The
Phi test result is given by:
 =
(
=
( 2 /
N)1/2 ,
2 /
N)1/2 ,
which assumes values in the range [-1,1]. That is,
 equals:
equals:
-1 when there is complete contra-association;
. 0 when there is no association; and
+1 when there is complete association.
Remark. Unfortunately, Phi can yield a result that
exceeeds unity when the input table exceeds four cells
(2 × 2 configuration). In such cases, we recommend the
following modification to Phi, called Cramer's V-test.
A-3.4. Cramer's V-Test.
The Cramer test adjusts the Phi test result for the number of
rows or columns in the input data table. This adjustment
depends upon the minimum of the number of rows and the number
of columns. Both Phi and Cramer-V are equivalent in a
2 × 2-cell table.
The associational tests described thus far can be extended to yield a more
powerful test of association, called Pearson correlation.
A-3.5. Pearson Product-Moment Correlation.
Correlation is a process whose result indicates the strength of a
relationship between two variables. Pearson Product-Moment Correlation
(PPMC) expresses this estimate of association in terms of a linear
function. Thus, PPMC is occasionally called zero-order correlation
or linear correlation.
- Algorithm. Let two images a,b
 RX be
correlated using PPMC. The resultant correlation coefficient
r is given by
RX be
correlated using PPMC. The resultant correlation coefficient
r is given by
|X| ·
 (a ·
b) -
(a ·
b) -
 a ·
a ·
 b
b
r = 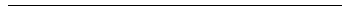 , (VI)
, (VI)
( |X| ·
 a2
- (
a2
- ( a)2
)1/2 ·
( |X| ·
a)2
)1/2 ·
( |X| ·
 b2
- (
b2
- ( b)2
)1/2
b)2
)1/2
where r varies over the interval [-1,1] such that:
-1 when there is complete contra-association;
. 0 when there is no association; and
+1 when there is complete association.
Note that r is also called the Pearson-r, Pearson
correlation coefficient, or Pearson-r coefficient.
Example. Let a and b be as shown in Table A-1,
which illustrates the first three steps involved in computing r.
Step 4 involves taking the sums of the columns in Table A-1.
Step 1 Step 2 Step 3
i a b a·b a2 b2
- --- --- ----- --- ----
1 12 9 81 144 81
2 4 8 32 16 64
3 3 10 30 9 100
4 6 1 6 36 1
5 7 4 28 49 16
6 1 6 7 1 36
--- --- ----- --- ----
 a=33
a=33  b=38
b=38  ab=184
ab=184  a2=255
a2=255  b2=298
b2=298
Table A-1. Initial steps in computing r(a,b).
Applying Equation (VI) to the result of Step 4, we obtain
6 · 184 - 33 · 38
r = 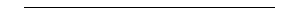 = -0.385 ,
= -0.385 ,
(6 · 255 - 332)1/2 ·
(6 · 298 - 382)1/2
which appears to indicate that the data are slightly
contra-associated.
Remark. The magnitude of r, not the sign, indicates the
strength of association between a and b.
Additionally,
an r2 value denotes the fraction of variance shared
by a and b. Thus, if
r = -0.385, then
r2 = 0.149, which indicates that 14.9 percent of the
variance in a is accounted for in b, and vice
versa.
Observation. It is possible to approximate the t-score
associated with a given Pearson correlation coefficient r, as
follows:
t = r · (N-2)/(1-r) .
In the previous example, N = |X|, the number of data
in a and b. Given that PPMC constitutes a
one-tailed test, and given a prespecified level of significance
0 < k < 1, we can look up tmin(N-2,k,T=1) in a table
of t-scores, where N-2 denotes the number of degrees of freedom.
If t < tmin, then the difference between a and
b is not statistically significant.
Remark. The Pearson-r coefficient is accurate for
linear correlation only. If the data have significant
nonlinearities, then other methods of comparison (e.g., least-
squares regression, analysis of variance, or template matching)
should be employed.
We next discuss simple methods by which one distribution can be made to
portray another distribution.
A-3.6. Transforming Probability Distributions.
- Observation. Occasionally, we encounter a
probability distribution that does not have a preferred form.
For example, suppose one prefers to convert a Poisson distribution
to a normal distribution that preserves the Poisson distribution's
mean and standard
deviation. There are two ways to implement this conversion:
- Analytical solution. One can substitute the
normal distribution into the Poisson distribution and solve
analytically to obtain the resultant conversion. Note that
boundary conditions for both distributions must be
satisfied.
- Histogram modification. One can think of both the
source and target distributions
in terms of their discrete histogram representations, then
use methods of histogram modification similar to those employed in
image processing. For example, given a source image a with
pixel values f
 [f1,fm], we
can modify the histogram h(a) to yield an image
whose distribution g(a) is based on the
pixel values e
[f1,fm], we
can modify the histogram h(a) to yield an image
whose distribution g(a) is based on the
pixel values e  [e1,em].
[e1,em].
For example, if c denotes the cumulative
histogram of a, then uniform histogram modification
is given by
e = [em - e1] · c(f) +
e1 .
Additional modification functions are cited in [Pra78].
Remark. If histogram modification is employed, then
the distribution of pixel values (symbols) in the resultant
image (message) will change. In the case of text symbols, this
could significantly change message semantics. As a result, a
cipher must generate spurious symbols that absorb the new
probabilities without changing message semantics. Such ciphers
are called homophones, and will be discussed later in
this class when we consider steganography.
We next discuss properties of the normal distribution.
- Observation. The integral of a distribution on a random
variable X is the cumulative distribution, which we have
seen has useful properties for computing order-statistical measures
such as the median. Similarly, the derivatives of a
distribution can have interesting properties, for example,
the following integral and derivatives of the normal distribution:
Remark.
Taking the derivative of a distribution is useful when automatically
comparing distributions via landmarks such as local maxima (e.g.,
in the case of multimodal distributions). For example, if one
has a bimodal distribution, one can detect the modes (peaks)
by detecting where the second derivative of the corresponding
histogram approaches zero from below. We will discuss this
technique further when we use histogram matching as a method of
cryptanalysis.
This concludes our discussion of basic statistics for this class.
Additional statistical concepts will be defined as they are introduced in
theory development.
References
[Dav94]
Davis, D., R. Ihaka, and P. Fenstermacher.
"Cryptographic randomness from air turbulence in disk drives",
in Yvo G. Desmedt, Ed., Proceedings CRYPTO 94,
Springer Lecture Notes in Computer Science 839:114-120 (1994).
[Let94] Lettington, A.H. and Q.H. Hong. "An interpolator for
infrared images", Optical Engineering 33:725-729 (1994).
[Mau91]
Maurer, U.M. "A universal statistical test for random bit generators",
In A.J. Menezes and S. A. Vanstone, Eds., Proceedings CRYPTO 90,
Springer Lecture Notes in Computer Science 537:409-420 (1991).
[Pra78]
Pratt, W. Digital Image Processing, New York: John Wiley (1978).
Copyright © 1996 by Mark S. Schmalz, All Rights Reserved
 RX
is given by
RX
is given by
 a / |X|
a / |X|
 (a) =
(
(a) =
( (a-µ)2 / |X| )1/2 ,
(a-µ)2 / |X| )1/2 ,
 2.
2.
 (a) is computed
according to the following steps:
(a) is computed
according to the following steps:
 (a) = 1.18034.
(a) = 1.18034.
 RX
is a map h
RX
is a map h  NF whose fth bin count
is given by:
NF whose fth bin count
is given by:

 =f (a) ,
f
=f (a) ,
f  F .
F .
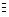 h(a)(A), then
h(A) = 5 since there are 5 A's in
Abracadabra. Additionally, h(B) = 2,
h(C) = 1, and so forth.
h(a)(A), then
h(A) = 5 since there are 5 A's in
Abracadabra. Additionally, h(B) = 2,
h(C) = 1, and so forth.
 (Zn)X, then
the histogram h(a) can be computed as:
(Zn)X, then
the histogram h(a) can be computed as:
 2 of
image a, as follows:
2 of
image a, as follows:
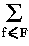 f · h(f) / |X|
f · h(f) / |X|
 2(a) =
2(a) =
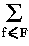 (f-µ)2 · h(f) / |X| .
(f-µ)2 · h(f) / |X| .
 h, where
f
h, where
f domain(h).
Alternatively, we can say that
f
domain(h).
Alternatively, we can say that
f range(a),
which implies that
range(a),
which implies that
 h .
h .
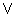 h.
For example, via Lebesque integration, h(a) could
be normalized to the unit interval
[0,1]
h.
For example, via Lebesque integration, h(a) could
be normalized to the unit interval
[0,1] R to yield
the following distribution of the values of a:
R to yield
the following distribution of the values of a:
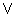 (h) .
(h) .
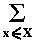 a(x) · xk / |X| .
a(x) · xk / |X| .

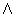 (domain(c || > |X|/2))
(domain(c || > |X|/2))
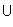 B) =
Pr(A) + Pr(B) .
B) =
Pr(A) + Pr(B) .

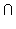 B).
B).

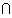 B = {b}, we have
B = {b}, we have
 .
. 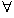 f
f
 .
.  )1/2
)1/2
 Pr(X=x) =
Pr(X=x) = 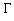 (a + 1)ba+1
(a + 1)ba+1

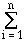 (Xi)2
(Xi)2  and the mean and
standard deviation are given by µ = n and
and the mean and
standard deviation are given by µ = n and  ,
,
 =
(
=
(
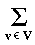 h(u,v) ,
u
h(u,v) ,
u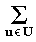 h(u,v) ,
v
h(u,v) ,
v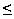 2 × 2 and
d = 1, then
2 × 2 and
d = 1, then
 =
(
=
(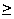 2. Cramer's V-test is
computed as:
2. Cramer's V-test is
computed as:
 , (VI)
, (VI)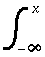 e-s2/2 ds .
e-s2/2 ds .
