Cryptology - I: Appendix B - Review of Information Theory

Instructors: R.E. Newman-Wolfe and M.S. Schmalz

Information theory is an important subdiscipline of mathematics that emerged from cryptologic research in the late 1940s. Primarily deriving from the work of Claude Shannon [Sha49] at Bell Laboratories, information theory provides a rigorous framework for modelling the content of messages in cryptology in terms of the number of bits required to encode each symbol.

In this section, we present an introduction to information theory that clarifies concepts of information theory and statistical encoding. For those who are more mathematically inclined, excellent discussions of information theory are given in [McE77] and [Ham86].

B-1. Entropy.

• Observation. Assume that processes P₁ and P₂ have n₁ and n₂ equiprobable outcomes, respectively. If the outputs of P₁ and P₂ are combined to yield the output of a process P₃, then P₃ has n₃ = n₁ · n₂ equiprobable outcomes. The computation of n₃ is described as follows.

  Assumption. Let P₁,P₂,P₃ : F -> F and let n₁ = |range(P₁)| with n₂ = |range(P₂)|. If P₃ is obtained from some function of the output of P₁ and P₂, then domain(P₃) range(P₁) × range(P₂). However, we previously assumed that range(P_i) = domain(P_i) for i = 1..3. The preceding expression can thus be rewritten as:

  range(P₃) range(P₁) × range(P₂),

  which implies that

  |range(P₃)| < |range(P₁)| · |range(P₂)| .

  In the limiting case, where the preceding relation is the equality relation, we have n₃ = n₁ · n₂.

  Observation. The amount of information output by a continually productive source is a strictly increasing function of time.

  Definition. Let H denote the information content (or entropy) of a process, and let H denote the operation that computes H. In the first Observation of this section, if H_i = H(P_i) for i = 1..3, then the entropy of P₃ is given by H₃ = H₁ + H₂.

• Assumption. Let the number of equiprobable outcomes of a process P : F -> F be determined by a function N : (F -> F) -> N, where domain(N) denotes a process. Assume that a function f combines two processes of form F -> F to yield a process of form F -> F. What analytically tractable function embodies the concept expressed in the composition N o f?

  Lemma 1. Given the preceding assumption and processes P₁,P₁ : F -> F, the entropy H(P₃) of a process P₃ = f(P₁,P₂) is given by

  H(P₃) = log(n₃) = log(N(P₃))

  if the following conditions are satisfied:
  1. P₁ and P₂ have equiprobable outcomes n₁ = N(P₁) and n₂ = N(P₂).
  2. P₃ has n₃ = n₁ · n₂ equiprobable outcomes.
  3. If H_i = H(P_i) for i = 1..3, then H₃ = H₁ + H₂.
  Proof. Assume that conditions 1-3 hold. Note that H = log is the only function that satisfies conditions 1-3 simultaneously, since n₃ = n₁ · n₂, H(P₃) = log(n₃) = log(N(P₃)), and

  log(n₃) = log(n₁·n₂) = log(n₁) + log(n₂) .

  Thus, if H = log, then H₃ = H₁ + H₂, and the lemma holds.

  Example. Let n₁ = N(P₁) = 32 and n₂ = N(P₂) = 64. It follows that H₁ = 5 and H₂ = 6. If n₃ = n₁ · n₂, then H₃ = H(P₃) = H₁ + H₂ = 11 bits. As a result, P₃ has 2¹¹ = 2048 possible outcomes.

  We next explore the case when two processes have outcomes that are not equiprobable.

• Remark. Suppose we have two processes P₁ and P₂ with n₁ and n₂ equiprobable outcomes. Let probabilities p₁ and p₂ be associated with n₁ and n₂, such that n = n₁ + n₂ and

  p_i = n_i/n , where i = 1,2 .

  Recall that the entropy associated with one message among n equally likely outcomes is denoted by H(n) = log(n). However, for n₁/n of the time, H(n₁) = log(n₁). Symmetrically, H(n₂) = log(n₂). Thus, the net entropy is given by

  H = log(n) - (n₁/n)·log(n₁) - (n₂/n)·log(n₂) ,

  which can be expressed in terms of probabilities as:

  H = -(p₁/n)·log(p₁) - (p₂/n)·log(p₂) .

  Since p₁,p₂ < 0, the logarithms are negative and H > 0.

Via the preceding equation, we can express information content in terms of a discrete probability distribution over a random variable. The following theorem is illustrative.

Theorem 2. Let a process P have n possible outcomes that exhibit individual probabilities p_i, where i = 1..n. The entropy of P, denoted by H(P), is given by

H(P) = 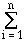-p_i · logp_i . (I)

Proof. The proof, which is well known, follows from the preceding remark and
induction on i.

We next restate the law of additive combination of information, with proof given in [Ham86] and [McE77].

• Theorem 3. If a process P is comprised of two statistically independent processes P₁ and P₂, then the entropy of P is given by

  H(P) = H(P₁) + H(P₂) .

  Theorem 4. If a process P is comprised of two processes P₁ and P₂ that are not statistically independent, then the entropy of P is given by

  H(P) < H(P₁) + H(P₂) .

  The following theorem of maximum information is stated without proof, which may be assigned as an exercise or as homework.

  Theorem 5. If a discrete process P has n outcomes that exhibit individual probabilities p_i, i = 1..n, then P yields maximum information when p_i = 1/n.

  Definition. If an alphabet has n symbols, then the average rate is given by log(n)/n bits per symbol.

  Example. The modern English alphabet F has 26 symbols plus the ten digits 0-9. Excluding the digits, H(F) = log(26) = 4.5 bits/symbol. If the probability of each letter is taken into account and we apply Equation (I), then H(F) < 4 bits/symbol. Using a text corpus abstracted from technical documents, Shannon showed that the actual information content of English is approximately one bit per symbol, since the nonuniform distribution of n-grams implies statistical dependence among symbols. In practice, various entropy values can be obtained using different text corpi expressed in other languages.

  We next discuss the computation of measures of information content in encrypted text.

  Example. Assume that the substitution cipher T : F^X × K -> F^X, where K is called the keyspace and T is one-to-one and onto. Let |F| = 26, as before, and let K = F. Recall from previous examples that there are 26! (i.e., |F|!) possible keys of length 26 symbols.

  Let us construct a 26-character key that encrypts a 40-character text (i.e., |X| = 40). The information content of the key is given by H_k = log(|F|!) = log(26!). If the plaintext has entropy
  H_t, then the substitution has entropy H(T) < H_t + H_k, since the plaintext and key may not be statistically independent.

  From Theorem 5, a 40-character text has maximum entropy

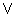  (H(T)) 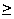H_t + H_k = H_t + log(26!) .

  Substituting the maximum entropy for H_t, we obtain:

  H_t 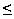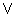(H_t) - H_k = 40 · log(26) - log(26)! = 100 bits .

  At 100 bits per 40 characters, we have an average rate of 2.5 bits per symbol, which is considerably less than the maximum information content of text (4 bits per symbol) computed in the preceding example.

B-2. Redundancy.

Digressing for a moment, we note that in data compression, one attempts to reduce the entropy of compressed data without losing required information. In order to compress data, we typically eliminate redundancy, which can be accomplished in a variety of ways. In cryptography, we also want to reduce redundancy where possible, since redundant information can increase the likelihood that a cryptanalyst would discover the information.

In this section, we briefly discuss measures of redundancy and apply such measures to various textual examples. The utility of this technique will become more apparent when we consider methods of cryptanalysis in Appendix C and discuss more advanced methodologies in the section on modern ciphers.

References.

[Ham86] Hamming, R.W. Coding and Information Theory, Englewood Cliffs, NJ: Prentice-Hall (1986).

[McE77] McEliece, R. The Theory of Information and Coding: A Mathematical Framework for Communication, Reading, MA: Addison-Wesley (1977).

[Pat87] Patterson, W. Mathematical Cryptology for Computer Scientists and Mathematicians, Totowa, NJ:Rowan and Littlefield (1987).

[Sha49] Shannon, C. Mathematical Theory of Communication, Urbana, IL: University of Illinois Press (1949).

This concludes our discussion of basic information theory. More involved concepts will be defined when they are introduced in theory development.