- Closure, meaning that the result of operation · is in F, which comprises the domain of · (i.e., domain(·) = F×F);
- Associativity, i.e.,
(f · g) · h = f · (g · h)
for all f,g,h
 F;
F;
- Identity e such that e · f
= f · e = f for all
f
 F; and
F; and
- Inverse: For each f
 F, there exists f-1
F, there exists f-1 F such that f · f-1 = f-1 · f = e.
F such that f · f-1 = f-1 · f = e.
Example. F = Z with addition (· = +) having identity e = 0, where f-1 = -f.
Example. F = Zn with addition
(· = +) taken modulo n, identity e = 0, and inverse
f-1 = n - f. Thus,
a+b 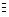 0 (resulting from mod n).
0 (resulting from mod n).
Example. Let F = Zp \ {0}, a prime number p, and a group G = (F,·) with the operation · taken modulo p. Observe that:
- By definition of modulo-p multiplication, · is closed over F.
- Multiplication modulo p is associative, i.e.,
f · g · h = f · g · h,
The proof of this assertion is left as an exercise for the reader.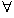 f,g,h
f,g,h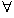 F.
F.
- Modulo-p multiplication has identity e = 1.
- For each f in F, there exists an inverse
f-1, such that
f · f-1 = e,
The proof of this assertion is left as an exercise for the reader.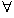 f
f F.
F.
Observation. If F = Zm \ {0}
and m is not prime, then there exists some x,y
 F such that x and
y have the same inverse. The proof is left as an
exercise to the reader.
F such that x and
y have the same inverse. The proof is left as an
exercise to the reader.
Remark. The reals with multiplication (R, ·) are not a group, because zero has no multiplicative inverse. However, (R\{0}, ·) and (R+, ·) are groups.
Definition. A subgroup G' =
(G,·) of a group G = (F,·)
is a group such that
G F.
F.
Example. (Q,·) is a subgroup of (R\{0},·) .
Example. (Z,+) is a subgroup of (Q,+).
Example. An onto mapping M: {1,2,3} -> {1,2,3} is exemplified by the graph G(M) = {(1,3), (1,2), (2,1)}.
Remark. It follows that, if M is an onto mapping, then p2(G(M)) = range(M), where p2 denotes projection onto the second coordinate.
Definition. A one-to-one mapping M : S -> S maps a given element of S to one and only one element of S.
Example. A one-to-one mapping M: {1,2,3} -> {1,2,3} is exemplified by the graph G(M) = {(1,3), (3,2), (2,1)}.
Definition. A bijection on F is a one-to-one and onto mapping.
Example. Let S = {a,b,c} and T = {1,2,3}. A bijection f: S -> T could have the graph G(f) = {(a,1),(b,3),(c,2)}. The mapping is one-to-one, i.e., each element of S maps uniquely to an element of T. Additionally, f is onto, since |G(f)| = |T|.
Example. Let S = {a,b,c} and T = {1,2,3}. Let f: S -> T have the graph G(f) = {(a,1),(b,1),(c,2)}. The mapping is not one-to-one, since two elements of S (a and b) map to the same element of T, namely, 1.
Example. Let S = {a,b,c} and T = {1,2,3,4}. The mapping f: S -> T cannot be a bijection, since the condition |T| > |S| obviates the onto property.
Definition. A permutation is a bijection. Example. Let S = {a,b,c} and let a = (a,c,b). If f is a permutation on S, then f(a) could have as its result (a,b,c) but not (a,a,c).
Definition. Let A be a set with n members, and let
S = { |
|
 : A -> A }
denote a set of permutations on A.
: A -> A }
denote a set of permutations on A.
Observation. G = (S,o) is a group, where o denotes functional composition.
One can prove the group properties of G, as follows:
- Closure. A permutation is a bijection. The composition of bijections is a bijection.
- Identity. Let the identity permutation
 (a) = a, where a denotes an
element of A. Given
(a) = a, where a denotes an
element of A. Given  1
1 S,
S,  o
o  1 =
1 =
 1 o
1 o  =
=  1, which is easily verified by inspection.
1, which is easily verified by inspection. - Associativity. This property follows from the fact that composition is associative.
- Inverse. Each permutation
 1
1
 S has an inverse
(
S has an inverse
( 1)-1,
1)-1,
 S such that
S such that
 1
o (
1
o ( 1)-1 =
1)-1 =  , the identity permutation.
, the identity permutation.
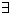 e
e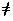 0
0

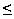 k. By Theorem 4,
char(F) is prime.
k. By Theorem 4,
char(F) is prime.
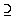 I
implies that J = I, or
I
implies that J = I, or 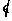 M then I = {af+m :
f
M then I = {af+m :
f M then I = F,
which implies that af+m = 1 for some
f
M then I = F,
which implies that af+m = 1 for some
f M and I
M and I
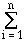 fi· xi,
f0,fi
fi· xi,
f0,fi fi·
xi, fi
fi·
xi, fi gi·
xi, gi
gi·
xi, gi (fi + gi) · xi + r ,
(fi + gi) · xi + r ,
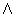 (m,n) and
(m,n) and
 gi · xi
gi · xi
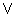 (m,n) if m > n,
and symmetrically (using f instead of g) if m < n.
(m,n) if m > n,
and symmetrically (using f instead of g) if m < n.