Intent:

This pattern addresses the question "Given a way of decomposing a problem into tasks and a way of collecting these tasks into logically related groups, how must these groups of tasks be ordered to satisfy constraints among tasks?"

Motivation:

This pattern constitutes the second step in analyzing dependencies among the tasks of a problem decomposition. The first step, addressed in the GroupTasks pattern, is to group tasks based on constraints among them. The next step, discussed here, is to help the designer find and correctly account for dependencies resulting from constraints on the order of execution of a collection of tasks.

Constraints among tasks fall into a few major categories (described in more detail in the GroupTasks pattern):

• Temporal dependencies, i.e., constraints placed on the order in which a collection of tasks executes.

• Requirements that particular tasks must execute at the same time (e.g., because each requires information that will be produced by the others).

• Lack of constraint, i.e., total independence. While this is not strictly speaking a constraint, it is an important feature of a set of tasks (because it means they can execute in any order, including concurrently), and it is important to clearly note when this holds.

The purpose of this design pattern is to help the designer find and correctly account for dependencies resulting from constraints on the order of execution of a collection of tasks.

Applicability:

Use this pattern when

• You have decomposed the problem into tasks and have decided where it makes sense to combine tasks into groups (as discussed in the GroupTasks pattern).

Implementation:

The goal of this pattern is to identify ordering constraints among groups of tasks and use them to define a partial ordering among task groups. There are two goals to be met in defining this ordering:

• It must be restrictive enough to satisfy all the constraints, to be sure the resulting design is correct.

• It should not be more restrictive than it needs to be. Unneeded constraints can impair program efficiency; the fewer the constraints, the more flexibility you have to shift tasks around to balance the computational load between processing elements.

To identify ordering constraints, consider the following ways tasks can depend on each other:

• First look at the data required by a group of tasks before they can execute. Once this data has been identified, find the task group that created it and you will have an order constraint. For example, if one group of tasks builds a complex data structure and another group uses it, you need to specify a sequential order constraint between these groups. In other words, when you combine these two groups in a program, they need to follow a sequential ordering.

• Also consider whether external services can impose ordering constraints. For example, if a program must write to a file in a certain order, then these file I/O operations likely impose an ordering constraint.

• Finally, it is equally important to note when an order constraint does not exist. If a number of task groups can execute independently, you have a much greater opportunity to exploit parallelism, so be sure to note when tasks are independent, not just when they are dependent.

Regardless of the source of the constraint, your task as a designer is the same. You must define the constraints that restrict the order of execution, and make sure they are handled correctly in the resulting algorithm. At the same time, you should note when ordering constraints are absent, since this will give you valuable flexibility later in your design.

Examples:

Molecular dynamics.

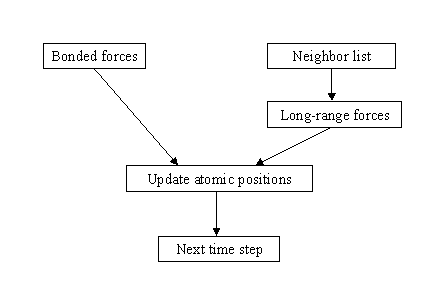
In the Examples section of the DependencyAnalysis pattern we described the problem of designing a parallel molecular dynamics program. In the GroupTasks pattern, we further described how to organize the tasks in the following groups:

• A group of tasks to find the "bonded forces" (vibrational forces and rotational forces) on each atom.

• A group of tasks to find the long-range forces on each atom.

• A group of tasks to update the position of each atom.

• A task to update the neighbor list for all the atoms (which trivially constitutes a task group).

Now we are ready to consider ordering constraints between the groups. Clearly, the update of the atomic positions cannot occur until the force computation is complete. Also, the long-range forces cannot be computed until the neighbor list is updated. So in each time step, the groups must be ordered as shown below FIX THIS.

While it is too early in the design to consider in detail how these ordering constraints will be enforced, eventually we will need to provide some sort of synchronization primitive to ensure that they are strictly followed.