Intent:

This pattern is used for parallel applications in which an apparently sequential operation on a recursive data is reworked to make it possible to operate on all elements of the data structure concurrently.

Also Known As:

• Pointer jumping, path doubling, reference following, and other strategies proposed in [JaJa92].

Motivation:

Most operations on recursive data structures (such as lists and trees) seem to have little exploitable concurrency, since one must follow the links that make up the data structure sequentially. However, it is sometimes possible to reshape such algorithms in a way that allows a program to operate concurrently on all elements of the data structure. [JaJa92] describes a number of such strategies for restructuring operations on lists and trees in a way that exposes such concurrency. To see how this works, consider the following example based on the pointer-jumping (path-doubling) strategy:

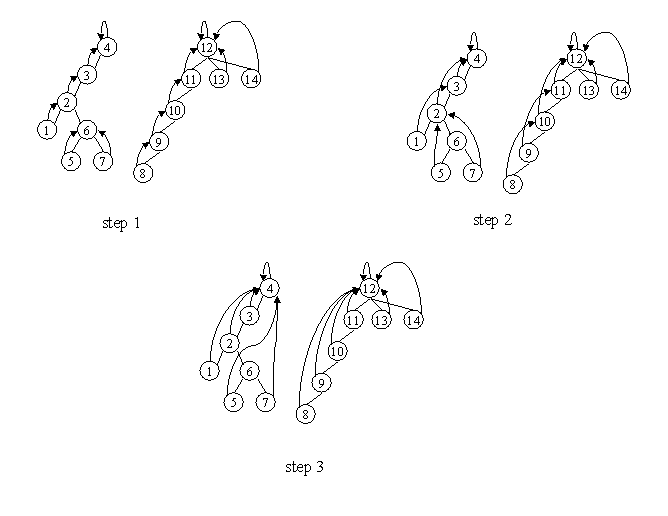
Suppose we have a forest of rooted directed trees (defined by specifying, for each node, its immediate ancestor -- with a root node's ancestor being itself) and want to compute, for each node in the forest, the root of the tree containing that node. To do this in a sequential program, we would probably trace depth-first through each tree from its root to its leaf nodes; as we visit each node, we have the needed information about the corresponding root. Total running time of such a program for a forest of N nodes would be O(N).

The approach proposed by JaJa uses his "pointer-jumping" strategy, which can be described as follows: The algorithm is based on a recursive data structure (usually a forest of rooted directed trees) and the repeated calculation of some relation between each node and its "successor". Initially each node's successor is its parent in the tree to which it belongs (which we can call "its ancestor 1 hop away"). At each step the successor is replaced by its successor (i.e., "the ancestor n hops away" is replaced by "the ancestor 2n hops away", hence the alternate name "path doubling"). We can also define additional variables for each node, such that whenever we update the node's successor, we also update these additional variables using data from the node and its successor.

We can apply this to the problem of finding roots as follows. Initially each node's "successor" is defined to be its parent. For each step, we calculate for every node its "successor's successor". (Here we do not need additional variables; the desired result will be found in the "successor" variables.) We note that for a node whose successor is the desired result (the root of the tree to which the node belongs), the successor and the successor's successor are the same (since a root's ancestor is itself), so we should continue the "for each step" process until it converges, i.e., until the values produced by one step are the same as the values produced by the preceding step. At most O(log N) steps are required, giving an execution time of O(log N). We observe, however, that the total amount of work required is now O(N log N)!

The following figure shows an example requiring three steps to converge. (In the figure, straight lines without arrows represent the original parent-child relationships among nodes, while curved lines with arrows point from nodes to their successors.)

An interesting aspect of this restructuring is that the new algorithm involves substantially more total work than the original sequential one, but the work can be spread among units of execution in such a way that the total running time is decreased; the same is true of most of the strategies this pattern represents. If one were to convert one of these algorithms directly back to a sequential form, the result would be quite inefficient.

Many of the resulting algorithms are quite clever, but their practical application may be limited by the following considerations:

• It must be possible to revise the implementation of the data structure to allow unit-time access to all elements. This generally means that the data structure must be implemented using arrays in some way rather than pointers alone.
• The concurrency is often extremely fine-grained, making this an impractical choice for many current programming environments.

We believe that situations in which this pattern would be useful in practical program development are quite rare.

In contrast to the high degree of cleverness involved in the restructuring of the algorithm, the actual concurrency is not very interesting. The basic structure of one of these algorithms is a sequential composition (possibly in the form of a loop), in which each element of the sequence can be described as "perform this operation on all (or selected) elements of the recursive data structure".

Applicability:

• As noted, we speculate that situations in which this pattern is useful in practical design are rare.

Structure:

Implementations of this pattern include the following key elements:

• A definition of the recursive data structure, plus what data is needed for each element of the structure.
• A definition of the concurrent operations to be performed (e.g., "replace each element's successor with its successor's successor").
• A definition of how these concurrent operations are composed to solve the whole problem (i.e., the top-level sequential program structure).
• A way of managing shared data.
• A way of scheduling the tasks onto units of execution (UEs).
• If the top-level structure involves a loop, a way of testing its termination condition.

Usage:

This pattern is typically used to provide high-level structure for an application; that is, the application is typically structured as an instance of this pattern.

Known Uses:

Several uses of this pattern are presented in [JaJa92].

Related Patterns:

With respect to the actual concurrency, this pattern is very much like GeometricDecomposition, the only difference being that here the data structure whose elements are to be operated on concurrently form (conceptually) a recursive data structure, which is not the case with GeometricDecomposition. What makes it different, we believe, is the emphasis on fundamental rethinking to expose unexpected fine-grained concurrency.