GIS - Computational Problems: § 1: GIS Features
The majority of GIS datasets are currently represented in vector format,
which is convenient due to storage efficiency but can be difficult
to manipulate analytically. To achieve tractability, vector format GIS
data is often rasterized (e.g., conformed to a grid-cell representation).
The processes involved in vectorization of map data as well as rasterization
of vector data have indiosyncratic errors that manifest as representational
error in a given GIS system.
Section Overview. In this section, for purposes of orientation,
we overview the vectorization of GIS data, then discuss theoretical and
practical issues associated with feature and dataset merging. It is important
to note that this section does not have as its goal the development
of a specific "best" technique or algorithm for performing vectorization
or rasterization operations. The material is structured as follows:
2.1. Polygonalization and Merging of Vector Data Sets
2.2. Determining Feature Type from GIS/Image Data
2.3. Resolving GIS Attribute Conflicts
2.4. Merging Disjoint Heterogeneous Regions
2.5. Coregistration of GIS Features and Neighborhoods
In Section 2.1, we outline basic problems in dealing with vector-format
GIS datasets, then discuss vectorization, rasterization, and dataset merging.
Sections 2.2 and 2.3 detail the unsolved problem of determining feature
type from map data, satellite imagery, etc., and resolving conflicting
feature types or attributes in rasterized vector datasets or grid-cell
data. Section 2.4 extends the preceding concepts to include the merging
of disjoint datasets for which some coordinate information is available.
Section 2.5 details a related sub-problem, namely, the coregistration of
map information, imagery, and GIS data.
Goals. For the purposes of this course, goals for this
section include:
- Learning GIS terminology and background;
- Exploring two dataset-related problems instantiated as
merging and alignment of vector- or raster-format
data;
- Understanding GIS feature types, attributes, and errors
inherent in GIS data, with the ability to estimate output error for
GIS algorithms when input error is known; and
- Prediction of computational cost and accuracy (e.g., the
space-time-error bandwidth product) for a given algorithm.
Orientation, Terminology, and Problems. The process of meeting
our goals will be more efficient if we understand some differences
between GIS and the better-established discipline of cartography or
map-making (which is often confused with GIS).
- Goals: Cartography emphasizes map-making with some
emphasis on analysis (e.g., derivation of map projections). In
contrast, GIS emphasizes storage, retrieval, and analysis of spatial
datasets.
- Basis: In cartography, map information is referenced to
a datum plane, whereas GIS seeks a common spatial domain to
(hopefully) minimize coregistration error when comparing multiple
spatial datasets.
- Key Problems: Cartographers seek to maintain map
databases with current, accuracy information, and render updates more
accurate as with improvement of land surveying and bathymetry
techniques (bathymetry = measurement of water depth). GIS
deals with these problems as well, but also emphasizes the
acquisition, formatting, merging, alignment, analysis, and reporting
of spatial data about land use, function, features and attributes,
etc.
GIS terms can often be confused with corresponding terminology and
notation in cartography. Hence, we offer the following definitions:
- Spatial Data are information about land or water that
are referenced to a spatial domain (e.g., map coordinates such as
latitude and longitude);
- Spectral Data comprise signals, imagery, or information
specific to one or more frequencies or wavelengths (e.g., passbands
in the electromagnetic spectrum);
- Resource Data comprise signals, imagery, or information
concerning the availability or use of natural or manmade resources
that are related to spatial (e.g., map) domains; and
- Coregistered Data are two or more datasets (a) whose
domains have a nonempty intersection W and (b) which have
corresponding features in each dataset aligned on the same point in
W.
Key Problems of Interest in this Section include the feature
conflict resolution problem and the dataset merging
problem. Exact or approximate solutions to these problems
discussed in this section are intended to support further research in
the higher-level problems of heterogeneous dataset merging and
alignment.
Assumption. Let there exist two GIS datasets a,b
 FX, where
F denotes the GIS dataset features and X
FX, where
F denotes the GIS dataset features and X
 Rn denotes
the dataset's spatial domain, with n = 2 customary.
Rn denotes
the dataset's spatial domain, with n = 2 customary.
- The Feature Correspondence Problem can be stated
as follows.
PFCP: If N : X -> 2X
denotes a neighborhood on X, then given a point x
 X, does
a point y
X, does
a point y  X
exist such that a|N(x) and
b|N(y) correlate better than
for any other choice of y?
X
exist such that a|N(x) and
b|N(y) correlate better than
for any other choice of y?
Extension: For each z
 X, determine
X, determine
d(z) = x(z) - y(z)
such that PFCP is satisfied. The resultant image
d  (Rn)X is called the
disparity map of a with respect to b.
(Rn)X is called the
disparity map of a with respect to b.
Definition: Given d, if a (or
b) is compensated for d to yield a (or
b), such that maximal correlation exists between
a|N(x) and
b|N(x) for each x
 X, then b and
a (a and b) are said to be
coregistered.
X, then b and
a (a and b) are said to be
coregistered.
- The Dataset Merging Problem can be stated as follows:
PDSM: Assume that there exists ground truth
ground truth g  FX and a comparison function c : F
× F -> R. If a(x)
FX and a comparison function c : F
× F -> R. If a(x)
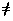 b(x) for
some x
b(x) for
some x  X, then what
mapping f : FX × FX
-> FX can be found (if any) such that the
representational error
X, then what
mapping f : FX × FX
-> FX can be found (if any) such that the
representational error
e = ||c(f(a,b), g)||
is minimized with respect to ||c(a,g)|| and
||c(b,g)||, where ||x|| denotes the norm
of x?
For example, if c is the subtraction operation, then
minimization could be subject to a constraint such as:
|e|  |c(a,g)| + |c(b,g)| .
|c(a,g)| + |c(b,g)| .
As an aside, note that in the extension of the corresponding points
problem, if the disparity map d is a constant image, then
coregistration can be a trivial process, provided that significant
data does not lie outside the common domain W. Otherwise, we
say that d represents nonuniform disparity. In cases
where the magnitude or direction component of the disparity d
is a nonlinear function of x, we say that there exists
anisomorphic disparity. For example, consider the simple cases
of optical distortions such as barrel distortion or
pincushion distortion, which nonlinearly warp an input image.
We next consider the processes of map segmentation into vector data
sets, as well as rasterization and merging of vector data sets.
2.1. Polygonalization and Merging of Vector Data Sets.
Given a scene as shown in Figure 2.1, a corresponding map a on
a two-dimensional domain
X  R2
contains |X| points x
R2
contains |X| points x
 X that may be expressed in
terms of the map coordinates (x,y)
X that may be expressed in
terms of the map coordinates (x,y)
 X. For example, one could
have the customary coordinates of latitude and longitude, or survey
measure from a given benchmark.
X. For example, one could
have the customary coordinates of latitude and longitude, or survey
measure from a given benchmark.

Figure 2.1. Schematic diagram of (a) natural scene and (b)
corresponding 2-D map.
A given domain point x  X customarily has measurement error associated with locating an
object on the map a. One way to express such error is via an
abstraction called Circular Error Probable (CEP), as shown in
Figure 2.2. For example, given North-South error
X customarily has measurement error associated with locating an
object on the map a. One way to express such error is via an
abstraction called Circular Error Probable (CEP), as shown in
Figure 2.2. For example, given North-South error
 NS
(sometimes called Northing error) or East-West error
NS
(sometimes called Northing error) or East-West error
 EW
(sometimes called Easting error), we can approximate CEP,
denoted by
EW
(sometimes called Easting error), we can approximate CEP,
denoted by  CEP,
as follows:
CEP,
as follows:
 CEP =
((
CEP =
(( NS2
+
NS2
+  EW2)/2)1/2 ,
EW2)/2)1/2 ,
which assumes RMS error accumulation that may or may not
hold in practice.

Figure 2.2. Schematic diagram of circular error probable.
The concept of statistical characterization of spatial error
will be important to our subsequent analyses of GIS data and
algorithm accuracy. In practice, spatial error propagates through
the various phases of GIS data acquisition and processing algorithms,
as shown in Figure 2.3. Hence, if we have analytical expressions for
the constituent processes shown in Figure 2.3, we can apply well-known
error analysis procedures to obtain error functions of these
processes, from which estimations of GIS dataset error can be made.

Figure 2.3. Schematic diagram of error propagation in a
GIS data acquisition, preprocessing, and storage system.
In order to better understand the mathematics of algorithms involved in
GIS data processing and archival, we present the following discussion of
vectorization and rasterization processes.
2.1.1. Overview of Vectorization and Rasterization
Map data can be converted to a more compact format that describes (a)
the boundary coordinates of regions within the map, and (b) the contents
of each region. By coercing each bounded region to have one and only one
feature type, one can construct a map from a set of boundary coordinates
to a set of feature types, which we call the vectorization map.
High-Level Vectorization Algorithm. In general, vectorization
proceeds according to the following steps:
Step 1. Locate and determine points on the source map that
contain given map features having known feature types and attributes
(e.g., land, water, buildings).
Step 2. Segment the map labelled in pointwise fashion in
Step 1 to yield polygonal regions, each of which contain one and only
one feature type or attribute set.
Step 3. Given the vertices of the polygons obtained in
Step 2, represent each polygon as a path whose segments are described
by their vertices. These path segments are called vectors and
may be straight or curvilinear. For example, ARC/INFO uses curvilinear
vectors that are circular arcs.
Step 4. Associate each polygon (represented as a chain
of vectors or their vertices) with the geature type and attributes
contained within the corresponding map region.
Step 5. Encode and store the output of Step 4. For example,
one could use ARC/INFO, ERDAS, or IDRISI format, and could store the
data to disk or digital tape.
Rasterizing might initially appear
to be the inverse of vectorization, since it might appear that one
merely converts between vector and map data, or vice versa. However,
this is an oversimplification that yields little information about the
subprocesses and errors that are idiosyncratic to each of these two
important and markedly distinct processes.
In particular, we note that vectorization is concerned primarily
with the spatial definition of map neighborhoods or regions in
terms of a set of vector components (e.g., line segments or arcs) that
delimit a region having one and only one feature type or attribute
set. In contrast, rasterization assumes a given spatial segmentation
scheme (e.g., an image pixel grid) that is not necessarily
data-dependent, then associates one or more feature types or attribute
sets per grid cell. A key problem in vectorization is accurately
portraying the region boundary with a limited set of vector
primitives, whereas rasterization can be seen as primarily emphasizing
the resolution of feature type or attribute conflicts within a fixed,
prespecified spatial framework.
Discussion. Vectorization is acustomary procedure that has many
different implementations. Errors inherent in vectorization include:
-
Alignment Errors that result, for example, from inaccurate alignment
of linear vectors with curved region boundaries;
-
Quantization Errors which arise primarily from the choice of error
bound when matching one or more vectors to curved region boundaries that
are subtended by the vector(s); and
-
Segmentation Errors produced by (a) incorrect labelling of the source
maps (often considered a systematic error), or (b) gross errors in vectorizing
a region boundary.
By choosing curvilinear vector segments or by decreasing the error bound,
it may be possible to reduce vector alignment and quantization errors,
albeit with increased computational cost. However, quantization errors,
which derive from Nyquists's sampling theorm, are generally considered
irreducible unless they can be averaged to zero over the course of a computation.
Although such errors still remain as local features of the GIS dataset,
they are considered (erroneously) to be "averaged out" over a larger area
of the dataset domain.
High-Level Rasterization Algorithm. The following steps are generally
employed in rasterization:
Step 1. Choose a resolution interval q  R.
R.
Step 2. Discretize or partition a 2-D spatial map domain X
into rectangular blocks of size q×q map units.
Step 3. Resolve feature type conflicts within each block or grid
cell on a case-by-case basis, using contextual information as required.
Step 4. Resolve any remaining feature attribute conflicts.
Discussion. Rasterization tends to have similar errors to those
exhibited by vectorization, which include:
-
Spatial Quantization Error due to the nonzero resolution interval
q; and
-
Feature Resolution Error that results from incorrect assignment
of feature type or attributes within a grid cell.
Note that quantization error derives from the Nyquist criterion (sampling
theory) and decreases as q approaches zero. Additionally, when two conflicting
feature types are present within a given grid cell, feature type or attribute
resolution errors are unavoidable.
Dataset Merging Problem. The dataset merging problem in GIS can
be stated as follows:
PDMP : Given multiple GIS datasets (vector or
raster format), merge data to form GIS dataset on a common spatial domain.
Inherent in the process of combining datasets is feature conflict resolution.
Assume, for purposes of simplicity, that each GIS dataset is registered
on a common, two-dimensional spatial domain X. Then, PDMP
can be reduced to the following question:
Given GIS datasets a,b  FX , with what probability does a(x)
= b(x) ?
FX , with what probability does a(x)
= b(x) ?
Inherent in this specification of PDMP is the assumption that
GIS data can be coregistered on a common spatial domain. Raster format
data (e.g., an MxN-pixel rectangularly-structured domain) is the domain
most commonly employed, which is also called grid cell format. Hence,
if a dataset is in raster format, it may have to be resampled to produce
a raster of different resolution. If the data is in vector format, then
rasterization may be required. Thus, we next examine vector-to-raster conversion
in detail.
2.1.2. Rasterization of Vector-format GIS Data.
We have previously shown that the rasterization problem can be
reduced to the problem of resolving which feature attribute a grid cell
should be labelled. Additionally, we discussed area-based methods for feature
label assignment. Three pertinent cases will be discussed in this section,
which are listed in increasing order of difficulty, as follows:
Case I. A vector segment crosses a grid cell, thereby partitioning
the cell into two convex polygons.
Case II. Multiple vector segments connected to form one polyline
cross a grid cell, thereby partitioning the cell into two polygons, neither
of which could be convex.
Case III. Multiple vector segments connected to form multiple
polylines cross a grid cell, thereby partitioning the cell into multiple
polygons.
Fortunately, the area of each polygonal partition of a grid cell can be
accurately computed in every case using a simple algorithm derived from
the plane geometric formula for the area of a trapezoid.
Recall. Given a trapezoid T having parallel sides of length
a and b and height h, the area of T is given by
< T > = h · (a + b)/2 .
Observation. If a given polygon A in a vectorized map can be
decomposed into trapezoids A1, A2, ...,
Ai, ..., An, each of which has parallel sides of
length ai and bi, with height
hi, then the area of A would be computed as:
< A > =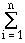 < Ai > =
< Ai > = 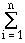 hi · (ai + bi)/2 .
hi · (ai + bi)/2 .
Applying this observation to Case I, we see that there are two sub-cases:
Case Ia: As shown in Figure ____b, given a bounded
map domain X  R2, a line segment belonging to the sequence of
segments that delimits a vector polygon is itself delimited by the
points xi,xi+1
R2, a line segment belonging to the sequence of
segments that delimits a vector polygon is itself delimited by the
points xi,xi+1
 X. Let the line
segment intersect the y-th grid cell in the rasterized
map domain Y
X. Let the line
segment intersect the y-th grid cell in the rasterized
map domain Y  Z2 at points zy(1) and
zy(2), thereby partitioning the grid cell into two
polygons A1 and A2. Given the vertices of the
grid cell denoted by xy(i)
Z2 at points zy(1) and
zy(2), thereby partitioning the grid cell into two
polygons A1 and A2. Given the vertices of the
grid cell denoted by xy(i)
 X,
i = 1..4, as shown in Figure ____b, the
parallel sides of the left-hand trapezoid have length
X,
i = 1..4, as shown in Figure ____b, the
parallel sides of the left-hand trapezoid have length
a1 = || xy(1) -
zy(1) || and b1 = ||
zy(2) - xy(3) ||
and height
h1 = || xy(2) -
xy(3) || .
Hence,
< A1 > = h1 ·
(a1 + b1)/2 ,
and symmetrically for the right-hand partition A2.
Case Ib: The grid cell is divided into a triangle and
an irregular pentagon, as shown in Figure ___b. Given the notational
conventions of Figure ___a, the area of the triangular partition
A1 is given by
< A1 > = ||
xy(1) - zy(1) || &183;
||xy(1) - zy(2) ||/2 ,
and the remaining are can be obtained by subtracting
< A1 > from the area of the grid cell.
In Case II, the grid cell is bisected by a sequence of line segments
whose vertices are given by the sequence S = {x1,
x2,..., xi, ...,
xn}  X. Each consecutive pair of vertices
xi,xi+1 defines the slant side of
a trapezoid, as shown in Figure ___a. Summing the areas of the
component trapezoids is a simple matter, unless the sequence reverses
direction, as shown in Figure ___b. In this case, we must employ a
more generalized algorithm for specifying the area of an irregular
polygon, as follows.
X. Each consecutive pair of vertices
xi,xi+1 defines the slant side of
a trapezoid, as shown in Figure ___a. Summing the areas of the
component trapezoids is a simple matter, unless the sequence reverses
direction, as shown in Figure ___b. In this case, we must employ a
more generalized algorithm for specifying the area of an irregular
polygon, as follows.
Algorithm. Given a map domain X R2, let the
image a ,
R2, let the
image a ,
%%%%LEFT OFF HERE%%%%
2.2. Determining Feature Type from GIS/Image Data.
2.3. Resolving GIS Attribute Conflicts.
2.4. Merging Disjoint Heterogeneous Regions.
2.5. Coregistration of GIS Features and Neighborhoods.
References.
{Doa97} Doaks, J. Another Introduction to GIS, New York:
Bogus Press (1997).
{Doe97} Doe, J.H. An Introduction to GIS, New York: Bogus
Press (1997).
This concludes our introductory discussion of GIS issues.
We next consider computational problems related to GIS features.
 FX, where
F denotes the GIS dataset features and X
FX, where
F denotes the GIS dataset features and X
 Rn denotes
the dataset's spatial domain, with n = 2 customary.
Rn denotes
the dataset's spatial domain, with n = 2 customary.  X, does
a point y
X, does
a point y  X
exist such that a|N(x) and
b|N(y) correlate better than
for any other choice of y?
X
exist such that a|N(x) and
b|N(y) correlate better than
for any other choice of y?
 X, determine
X, determine  (Rn)X is called the
disparity map of a with respect to b.
(Rn)X is called the
disparity map of a with respect to b.
 X, then b and
a (a and b) are said to be
coregistered.
X, then b and
a (a and b) are said to be
coregistered.
 FX and a comparison function c : F
× F -> R. If a(x)
FX and a comparison function c : F
× F -> R. If a(x)
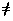 b(x) for
some x
b(x) for
some x  X, then what
mapping f : FX × FX
-> FX can be found (if any) such that the
representational error
X, then what
mapping f : FX × FX
-> FX can be found (if any) such that the
representational error
 |c(a,g)| + |c(b,g)| .
|c(a,g)| + |c(b,g)| .

 NS
(sometimes called Northing error) or East-West error
NS
(sometimes called Northing error) or East-West error


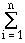 < Ai > =
< Ai > =