(This material is based upon work supported by the National Science Foundation (NSF) under Grant No. 0347574. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.)
Nowadays a large amount of (non-standard) applications are dealing with data characterized by spatial, temporal, and/or uncertain features. Examples of application fields interested in these kinds of data are Geographical Information Systems (GIS), geography, soil science, hydrology, meteorology, urban planning, environmental systems, mobile computing, forest fire management, multimedia applications, artificial intelligence, cognitive science, linguistics, to name only a few.
Special tasks and challenges arise if large volumes of these non-standard data have to be processed. An old and well known tool, which is tailored to these tasks, are database systems. But so far they are mainly specialized to the handling of so-called "standard" alphanumerical data like integers, reals, strings, and booleans. They as well as operations on them like addition, multiplication, string comparison, and equality test are rather simple and well understood. Non-standard data like spatial, temporal, multimedia, video, or genomics data have an inner, complex structure requiring sophisticated data representations, and their operations necessitate sophisticated and efficient algorithms.
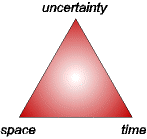
This project, which consists of a number of subprojects, aims at developing type systems (algebras) with respect to space, time, and uncertainty management, and embedding them into extensible database management systems. Especially, the combination of the three different features increases the problem complexity and leads to further research challenges. Our ultimate goal amounts to an integrated treatment of space, time, and uncertainty (STU) in a database context. This is illustrated by the following figure. It visualizes a main research goal for the future, namely to combine these three features and to reach the center of the triangle.

In detail, we are interested in the following topics:
Two-dimensional spatial data handling (related work)
Spatial data types and operations
Topological relationships between complex spatial objects
Spatial partitions (maps)
Spatially embedded graphs (networks)
Uncertain two-dimensional spatial data handling (related work)
Vague spatial data types and operations
Topological relationships between complex vague spatial objects
Fuzzy spatial data types and operations
Topological relationships between complex fuzzy spatial objects
Spatio-temporal data handling (related work)
Spatio-temporal data types and operations for moving objects
Spatio-temporal predicates and developments
Three-dimensional spatial data handling (related work)
In the following, we give some examples for data with all possible feature combinations:
Data with spatial or geometric features are usually called spatial objects. Spatial data in two-dimensional (2D) and three-dimensional (3D) space are distinguished. Spatial data in 2D space refer either to the location of an entity (like the position of a city on a map, the coordinates of a junction, or the position of the Eiffeltower) and are then called points, or, in addition, to the geometric extent of an entity, either as a line (like a road, a border, or a power line) or as a region (like the country USA, the state Florida, or the UF campus). Spatial data in 3D space refer to points, line, and regions in 3D space as well as to volumes (like buildings or mountains), surfaces, and reliefs. Examples of important operations on spatial objects are geometric intersection, union, and difference as well as metric operations like area, perimeter, and length. Another important class of operators are topological predicates characterizing the relative position of spatial objects to each other like overlap, meet, disjoint, inside, or equal. Collections of spatial objects can be subject to topological constraints. Collections with pairwise disjoint or adjacent regions form a partition of subdivision of space and are usually called maps (e.g., the map of the USA). The most important operation on maps besides many others is certainly map overlay which geometry intersects two or more maps into a single map. Collections of lines can form a spatially embedded graph and are usually called networks (like transportation networks). Here the shortest path operation, which computes the shortest way from a source to a destination, plays an important role.
Data with temporal features are usually called facts. Here the development of facts over time is of interest. An example is the increase of the salary of an employee over time. Almost all facts develop in a stepwise constant manner, i.e., a fact is always valid and constant for a time period and then at a certain time instant a discrete change occurs.
(Non-spatial, non-temporal) Data with uncertain features can be afflicted with different kinds of uncertainty like vagueness, fuzziness, or imprecision. Although we admit all interpretations of uncertainty, we mainly focus on fuzziness as an inherent property of entities and facts. Examples are statements like "John is tall." or "The weather is rather nice." In everyday life we all the time use these phrases afflicted with uncertainty like "tall", "nice", or "rather" and nevertheless have a rather clear or at least rough imagination and understanding of the underlying cognitive concepts. The integration of such concepts into database systems and their query languages is therefore a worthwhile goal.
Data with spatial and temporal features are usually called spatio-temporal objects. If a spatial object changes over time, it moves. If only the change of location is of interest, we speak of a moving point. Examples are the motion of a car, the walk of a human being, or the trajectory of a moving plane. If in addition the extent is relevant which can shrink or grow over time, we speak of a moving region. Examples are the evolution of air-polluted areas over time, the changing intensity of a magnetic field, or the motion of the lava of a volcanic eruption. The essential property of movement is that it is continuous. Operations on moving objects include the intersection, union, and difference of object evolutions, spatial and temporal projection operations, and many more. In particular, all spatial operations can be temporally lifted to the spatio-temporal domain. The movement of two spatial objects induces modifications of their mutual topological predicates over time which leads to a concept of spatio-temporal predicates.
Data with spatial and uncertain (fuzzy) features are usually called fuzzy spatial objects. Fuzziness is an inherent feature of many "natural" spatial phenomena which are not man-made. Examples of fuzzy spatial objects are the Indian ocean, which certainly has an extent that can unfortunately not uniquely and precisely determined or is unknown, or South England, or the transition between a valley and a mountain. Concepts like "far away", "rather near", or "predominantly overlapping" have a vague and fuzzy character. Fuzzy versions of crisp spatial operations and predicates are, of course, also here of interest.
Data with temporal and uncertain features are usually called uncertain statements. The statement "The election will be won by party X." is an example of such an uncertain statement.
Data with spatial, temporal, and uncertain (fuzzy) features will be called spatio-temporal fuzzy spatial objects. Application examples for them are temperature zones, hurricanes, or forest fires evolving dynamically over time and having a very fuzzy shape. Research on this feature combination will have to be done in the future.
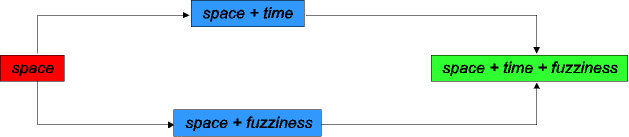
The following figure shows features and feature combinations for which the group has already done some research and gained some expertise. The objective of an integrated treatment of spatial, temporal, and uncertain features is expressed in the right part of the figure.